Un consultor de salud desea comparar las calificaciones de satisfacción de los pacientes de dos hospitales. El consultor recolecta calificaciones de 20 pacientes de cada uno de los hospitales.
El consultor realiza una prueba de 2 varianzas para determinar si las desviaciones estándar en las calificaciones de los pacientes de los dos hospitales son diferentes.
- Abra los datos de muestra, CompHospitales.MWX.
- Elija .
- En la lista desplegable, seleccione Ambas muestras están en una columna.
- En Muestras, ingrese Calificación.
- En ID de muestras, ingrese Hospital.
- Haga clic en Aceptar.
Interpretar los resultados
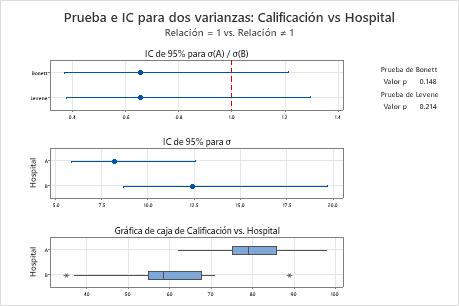
La hipótesis nula indica que la relación entre las desviaciones estándar es 1. Puesto que ambos valores p son mayores que el nivel de significancia (denotado como α o alfa) de 0,05, el consultor no puede rechazar la hipótesis nula. El consultor no tiene suficiente evidencia para concluir que las desviaciones estándar entre los hospitales son diferentes.
Método
| σ₁: desviación estándar de Calificación cuando Hospital = A |
|---|
| σ₂: desviación estándar de Calificación cuando Hospital = B |
| Relación: σ₁/σ₂ |
| Los métodos de Bonett y Levene son válidos para cualquier distribución continua. |
Estadísticas descriptivas
| Hospital | N | Desv.Est. | Varianza | IC de 95% para σ |
|---|---|---|---|---|
| A | 20 | 8.183 | 66.958 | (5.893, 12.597) |
| B | 20 | 12.431 | 154.537 | (8.693, 19.709) |
Relación de desviaciones estándar
| Relación estimada | IC de 95% para la relación usando Bonett | IC de 95% para la relación usando Levene |
|---|---|---|
| 0.658241 | (0.372, 1.215) | (0.378, 1.296) |
Prueba
| Hipótesis nula | H₀: σ₁ / σ₂ = 1 |
|---|---|
| Hipótesis alterna | H₁: σ₁ / σ₂ ≠ 1 |
| Nivel de significancia | α = 0.05 |
| Método | Estadística de prueba | GL1 | GL2 | Valor p |
|---|---|---|---|---|
| Bonett | 2.09 | 1 | 0.148 | |
| Levene | 1.60 | 1 | 38 | 0.214 |