En este tema
- Estadísticos
- Prueba de hipótesis para una diferencia en las tasas para la aproximación a la normal
- Prueba de hipótesis para una diferencia en las tasas para el método exacto
- Prueba de hipótesis para una diferencia en las tasas con el método de tasas agrupadas
- Prueba de hipótesis para una diferencia en las medias para el método de aproximación a la normal
- Prueba de hipótesis para una diferencia en las medias para el método exacto
- Prueba de hipótesis para una diferencia en las medias para el método de medias agrupadas
- Intervalo de confianza para la diferencia en las tasas
- Límites de confianza para la diferencia en las tasas
- Intervalo de confianza para la diferencia en las medias
- Límites de confianza para la diferencia en las medias
Estadísticos
| Término | Description |
|---|---|
| tasa de ocurrencia para la muestra i |
 |
| Término | Description |
|---|---|
| número medio de ocurrencias en la muestra i |
 |
Prueba de hipótesis para una diferencia en las tasas para la aproximación a la normal
Fórmula
La prueba de aproximación a la normal se basa en el siguiente estadístico Z, que se distribuye aproximadamente como una distribución normal estándar bajo la siguiente hipótesis nula:
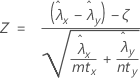
Minitab utiliza las siguientes ecuaciones del valor p para las hipótesis alternativas respectivas:



Notación
| Término | Description |
|---|---|
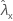 | valor observado de la tasa para la muestra X |
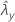 | valor observado de la tasa para la muestra Y |
| ζ | valor real de la diferencia entre las tasas de población de dos muestras |
| ζ0 | valor hipotético de la diferencia entre las tasas de población de dos muestras |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
| tx | longitud de la muestra X |
| ty | longitud de la muestra Y |
Prueba de hipótesis para una diferencia en las tasas para el método exacto
Fórmula
Cuando la diferencia hipotética es igual a 0, Minitab utiliza un procedimiento exacto para probar la siguiente hipótesis nula:
H0: ζ = λx – λy = 0 o H0: λx = λy
El procedimiento exacto se basa en el siguiente hecho, presuponiendo que la hipótesis nula es verdadera:
S | W ~ Binomial(w, p)
donde:


W = S + U


-
H1: ζ > 0: valor p = P(S ≥ s | w = s + u, p = p0)
-
H1: ζ < 0: valor p = P(S ≤ s | w = s + u, p = p0)
- H1: ζ ≠ 0:
- si P(S ≤ s | w = s + u, p = p0) ≤ 0.5 o P(S ≥ s | w = s + u, p = p0) ≤ 0.5
entonces el valor p = 2 × min {P(S ≤ s | w = s + u, p = p0), P(S ≥ s | w = s + u, p = p0)}
- de lo contrario, el valor p = 1.0
- si P(S ≤ s | w = s + u, p = p0) ≤ 0.5 o P(S ≥ s | w = s + u, p = p0) ≤ 0.5
donde:

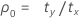
Notación
| Término | Description |
|---|---|
 | valor observado de la tasa para la muestra X |
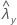 | valor observado de la tasa para la muestra Y |
| λx | valor real de la tasa para la población X |
| λy | valor real de la tasa para la población Y |
| ζ | valor real de la diferencia entre las tasas de población de dos muestras |
| tx | longitud de la muestra X |
| ty | longitud de la muestra Y |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
Prueba de hipótesis para una diferencia en las tasas con el método de tasas agrupadas
Cuando usted prueba una diferencia de cero con la siguiente hipótesis nula, tiene la opción de utilizar una tasa agrupada para ambas muestras:

Fórmula
El procedimiento de tasa agrupada se basa en el siguiente estadístico Z, que se distribuye aproximadamente como una distribución normal estándar bajo la siguiente hipótesis nula:
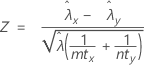
donde:
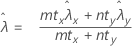
Minitab utiliza las siguientes ecuaciones del valor p para las hipótesis alternativas respectivas:


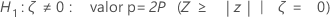
Notación
| Término | Description |
|---|---|
 | valor observado de la tasa para la muestra X |
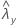 | valor observado de la tasa para la muestra Y |
| λx | valor real de la tasa para la población X |
| λy | valor verdadero de la tasa para la población Y |
| ζ | valor real de la diferencia entre las tasas de población de dos muestras |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
| tx | longitud de la muestra X |
| ty | longitud de la muestra Y |
Prueba de hipótesis para una diferencia en las medias para el método de aproximación a la normal
Fórmula
La prueba de aproximación a la normal se basa en el siguiente estadístico Z, que se distribuye aproximadamente como una distribución normal estándar bajo la siguiente hipótesis nula.
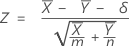
Minitab utiliza las siguientes ecuaciones del valor p para las hipótesis alternativas respectivas:



Notación
| Término | Description |
|---|---|
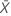 | valor observado del número medio de ocurrencias en la muestra X |
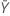 | valor observado del número medio de ocurrencias en la muestra Y |
| δ | valor real de la diferencia entre las medias de población de dos muestras |
| δ 0 | valor hipotético de la diferencia entre las medias de población de dos muestras |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
Prueba de hipótesis para una diferencia en las medias para el método exacto
Fórmula

El procedimiento exacto se basa en el siguiente hecho, presuponiendo que la hipótesis nula es verdadera:
S | W ~ Binomial(w, p)
donde:


W = S + U
Minitab utiliza las siguientes ecuaciones del valor p para las hipótesis alternativas respectivas:
H1: δ > 0: valor p = P(S ≥ s | w = s + u, δ = 0)
H1: δ < 0: valor p = P(S ≤ s | w = s + u, δ = 0)
-
Si P(S ≤ s|w = s + u, δ = 0) ≤ 0.5
o P(S ≥ s|w = s + u, δ = 0) ≤ 0.5
entonces:
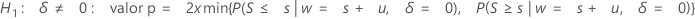
- de lo contrario, el valor p = 1.0
Una prueba de dos colas no es una prueba de colas iguales a menos que m = n.
Notación
| Término | Description |
|---|---|
| μx | valor real del número medio de ocurrencias en la población X |
| μy | valor real del número medio de ocurrencias en la población Y |
| δ | valor real de la diferencia entre las medias de población de dos muestras |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
Prueba de hipótesis para una diferencia en las medias para el método de medias agrupadas
Fórmula

El procedimiento de media agrupada se basa en el siguiente valor de Z, que se distribuye aproximadamente como una distribución normal estándar bajo la siguiente hipótesis nula:
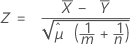
donde:
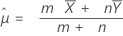
Minitab utiliza las siguientes ecuaciones del valor p para las hipótesis alternativas respectivas:

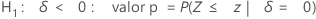

Notación
| Término | Description |
|---|---|
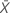 | valor observado del número medio de ocurrencias en la muestra X |
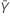 | valor observado del número medio de ocurrencias en la muestra Y |
| µx | valor real del número medio de ocurrencias en la población X |
| µy | valor real del número medio de ocurrencias en la población Y |
| δ | valor real de la diferencia entre las medias de población de dos muestras |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
Intervalo de confianza para la diferencia en las tasas
Fórmula
Un intervalo de confianza de 100(1 – α)% para la diferencia entre dos tasas de Poisson de población viene dado por:
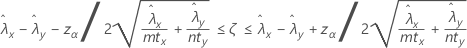
Notación
| Término | Description |
|---|---|
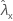 | valor observado de la tasa para la muestra X |
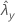 | valor observado de la tasa para la muestra Y |
| ζ | valor real de la diferencia entre las tasas de población de dos muestras |
| zx | punto percentil superior x de la distribución normal estándar, donde 0 < x < 1 |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
| tx | longitud de la muestra X |
| ty | longitud de la muestra Y |
Límites de confianza para la diferencia en las tasas
Fórmula
Cuando usted especifica una prueba del tipo "mayor que", un límite de confianza inferior de 100(1 – α)% para la diferencia entre dos tasas de Poisson de población viene dado por:
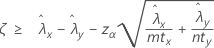
Cuando usted especifica una prueba del tipo "menor que", un límite de confianza superior de 100(1 – α)% para la diferencia entre dos tasas de Poisson de población viene dado por:
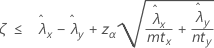
Notación
| Término | Description |
|---|---|
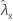 | valor observado de la tasa para la muestra X |
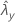 | valor observado de la tasa para la muestra Y |
| ζ | valor real de la diferencia entre las tasas de población de dos muestras |
| zx | el punto percentil superior x en la distribución normal estándar, donde 0 < x < 1 |
| m | tamaño de la muestra X |
| n | Tamaño de la muestra Y |
| tx | longitud de la muestra X |
| ty | longitud de la muestra Y |
Intervalo de confianza para la diferencia en las medias
Fórmula
Un intervalo de confianza de 100(1 – α)% para la diferencia entre dos medias de Poisson de población viene dado por:
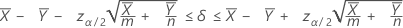
Notación
| Término | Description |
|---|---|
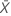 | valor observado del número medio de ocurrencias en la muestra X |
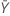 | valor observado del número medio de ocurrencias en la muestra Y |
| δ | valor real de la diferencia entre las medias de población de dos muestras |
| zx | punto percentil superior x en la distribución normal estándar, donde 0 < x < 1 |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
Límites de confianza para la diferencia en las medias
Fórmula
Cuando usted especifica una prueba del tipo "mayor que", un límite de confianza inferior de 100(1 – α)% para la diferencia entre dos medias de Poisson de población viene dado por:
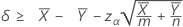
Cuando usted especifica una prueba del tipo "menor que", un límite de confianza superior de 100(1 – α)% para la diferencia entre dos medias de Poisson de población viene dado por:
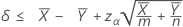
Notación
| Término | Description |
|---|---|
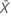 | valor observado del número medio de ocurrencias en la muestra X |
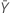 | valor observado del número medio de ocurrencias en la muestra Y |
| δ | valor real de la diferencia entre las medias de población de dos muestras |
| zx | punto percentil superior x en la distribución normal estándar, donde 0 < x < 1 |
| m | tamaño de la muestra X |
| n | tamaño de la muestra Y |
