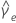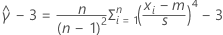En este tema
Desviación estándar (Desv.Est.)
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. La desviación estándar de la muestra es igual a la raíz cuadrada de la varianza de la muestra.
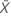 , entonces la desviación estándar viene dada por:
, entonces la desviación estándar viene dada por:

Notación
| Término | Description |
|---|---|
| xi | la iésima observación en la muestra |
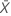 | la media de la muestra |
| S | la desviación estándar de la muestra |
| n | tamaño de la muestra |
Varianza
La varianza mide qué tan dispersos están los datos alrededor de su media. La varianza es igual a la desviación estándar elevada al cuadrado.
Fórmula
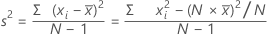
Notación
| Término | Description |
|---|---|
| xi | iésima observación |
 | media de las observaciones |
| N | número de observaciones presentes |
Intervalos y límites de confianza para el método de chi-cuadrada
Intervalos de confianza
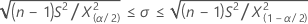

Límites de confianza
Cuando usted especifica una prueba unilateral, Minitab calcula un límite de confianza unilateral de 100(1–α)%, de acuerdo con la dirección de la hipótesis alternativa.
- Si usted especifica una hipótesis alternativa del tipo "mayor que", un límite inferior de 100(1–α)% para la desviación estándar de la población viene dado por:

Un límite inferior de 100(1–α)% para la varianza de la población viene dado por:
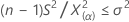
- Si usted especifica una hipótesis alternativa del tipo "menor que", un límite superior de 100(1–α)% para la desviación estándar de la población viene dado por:

Un límite superior de 100(1–α)% para la varianza de la población viene dado por:

Notación
| Término | Description |
|---|---|
| α | nivel de significancia para el intervalo de confianza de 100(1 – α)% |
| n | tamaño de la muestra |
| S2 | varianza de la muestra |
| Χ2(p) | el punto percentil superior 100pésimo en una distribución de chi-cuadrada con (n – 1) grados de libertad |
| σ | valor real de la desviación estándar de la población |
| σ2 | valor real de la varianza de la población |
Intervalos y límites de confianza para el método de Bonett
Utilice este método para cualquier tipo de datos continuos (normales o no normales) 1
Intervalo de confianza
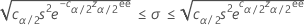
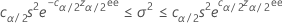
Límites de confianza
Cuando usted especifica una prueba unilateral, Minitab calcula un límite de confianza unilateral de 100(1–α)%, de acuerdo con la dirección de la hipótesis alternativa.
-
Si usted especifica una hipótesis alternativa del tipo "mayor que", un límite inferior de 100(1–α)% para la desviación estándar de la población viene dado por:
 Un límite inferior aproximado de 100(1- a)% para la varianza de la población viene dado por:
Un límite inferior aproximado de 100(1- a)% para la varianza de la población viene dado por:
-
Si usted especifica una hipótesis alternativa del tipo "menor que", un límite superior aproximado de 100(1–α)% para la desviación estándar de la población viene dado por:
 Un límite superior aproximado de 100(1- a)% para la varianza de la población viene dado por:
Un límite superior aproximado de 100(1- a)% para la varianza de la población viene dado por:
Notación
| Término | Description |
|---|---|
| α | 1 – nivel de confianza / 100 |
| cα/2 | n / (n – zα/2) |
| cα | n / (n – zα ) |
| s2 | valor observado de la varianza de la muestra |
| zα/2 | probabilidad acumulada inversa de la distribución normal estándar en 1 – α/2. Si n es menor que o igual a zα/2, Minitab no calcula los intervalos de confianza de Bonett. |
| zα | probabilidad acumulada inversa de la distribución normal estándar en 1 – α. Si n es menor que o igual a zα , Minitab no calcula los intervalos de confianza de Bonett. |
| ee |  |
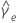 | 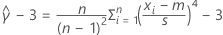 = curtosis excesiva estimada = curtosis excesiva estimada |
| m | media recortada con proporción de recorte igual a  ; m = media de la muestra cuando n es menor que o igual a 5 ; m = media de la muestra cuando n es menor que o igual a 5 |
| σ | valor real de la desviación estándar de la población |
| σ2 | valor real de la varianza de la población |
Prueba de hipótesis para el método de chi-cuadrada
Fórmula
La prueba de hipótesis utiliza las siguientes ecuaciones del valor p para las hipótesis alternativas respectivas:
H1: σ2 > σ02: valor p = P(Χ2 ≥ x2)
H1: σ2 < σ02: valor p = P(Χ2 ≤ x2)
H1: σ2 ≠ σ02: valor p = 2 × min{P(Χ2 ≤ x2), P(Χ2 ≥ x2)}
Notación
| Término | Description | ||||||
|---|---|---|---|---|---|---|---|
| σ2 | valor real de la varianza de población | ||||||
| σ02 | valor hipotético de la varianza de población | ||||||
| Χ2 | sigue una distribución de chi-cuadrada con (n – 1) grados de libertad cuando σ2 = σ02 | ||||||
| x2 | 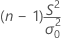
|
Prueba de hipótesis para el método de Bonett
Fórmula
El procedimiento de Bonett no está asociado con un estadístico de prueba. Sin embargo, Minitab utiliza las regiones de rechazo definidas por los límites de confianza para calcular un valor p.
Para una hipótesis bilateral, el valor p viene dado por:
p = 2 × min(αL, αU)
- Para una hipótesis alternativa del tipo "menor que", el valor p se calcula como αU después de reemplazar α/2 por α en la notación.
- Para una hipótesis alternativa del tipo "mayor que", el valor p se calcula como αL después de reemplazar α/2 por α en la notación.
Notación
| Término | Description | ||||||
|---|---|---|---|---|---|---|---|
| σ02 | varianza hipotética | ||||||
| αL | solución más pequeña, α, de la ecuación
 | ||||||
| αU | solución más pequeña, α, de la ecuación
 | ||||||
| cα/2 | n / (n – zα/2) | ||||||
| α | 1 – nivel de confianza / 100 | ||||||
| s2 | valor observado de la varianza de la muestra | ||||||
| zα/2 | probabilidad acumulada inversa de la distribución normal estándar en 1 – α/2. Si n es menor que o igual a zα/2, Minitab no calcula los intervalos de confianza de Bonett. | ||||||
| ee | 
|