En este tema
Paso 1: Determinar un intervalo de confianza para la media de la población
Primero, considere la media de la muestra y luego examine el intervalo de confianza.
La media de los datos de la muestra es una estimación de la media de la población. Puesto que la media se basa en los datos de una muestra y no en toda la población, es improbable que la media de la muestra sea igual a la media de la población. Para estimar mejor la media de la población, utilice el intervalo de confianza.
El intervalo de confianza proporciona un rango de valores probables para la media de la población. Por ejemplo, un nivel de confianza de 95% indica que si usted toma 100 muestras aleatorias de la población, podría esperar que aproximadamente 95 de las muestras produzcan intervalos que contengan la media de población. El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra. Para obtener más información, vaya a Maneras de obtener un intervalo de confianza más preciso.
Estadísticas descriptivas
| N | Media | Desv.Est. | Error estándar de la media | IC de 95% para μ |
|---|---|---|---|---|
| 25 | 330.6 | 154.2 | 30.8 | (266.9, 394.2) |
Resultados clave: Media, IC de 95%
En estos resultados, la estimación de la media de la población para el costo de energía es 330.6. Usted puede estar 95% seguro de que la media de la población está entre 266.9 y 394.2.
Paso 2: Determinar si los resultados de la prueba son estadísticamente significativos
- Valor p ≤ α: La diferencia entre las medias es estadísticamente significativa (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula. Usted puede concluir que la diferencia entre la media de población y la medida hipotética es estadísticamente significativa. Utilice su conocimiento especializado para determinar si la diferencia es significativa desde el punto de vista práctico. Para obtener más información, vaya a Significancia estadística y práctica.
- Valor p > α: La diferencia entre las medias no es estadísticamente significativa (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que la diferencia entre la media de la población y la media hipotética es estadísticamente significativa. Debe asegurarse de que su prueba tenga suficiente potencia para detectar una diferencia que es significativa desde el punto de vista práctico. Para obtener más información, vaya a Potencia y tamaño de la muestra para t de 1 muestra.
Estadísticas descriptivas
| N | Media | Desv.Est. | Error estándar de la media | IC de 95% para μ |
|---|---|---|---|---|
| 25 | 330.6 | 154.2 | 30.8 | (266.9, 394.2) |
Prueba
| Hipótesis nula | H₀: μ = 200 |
|---|---|
| Hipótesis alterna | H₁: μ ≠ 200 |
| Valor T | Valor p |
|---|---|
| 4.23 | 0.000 |
Resultado clave: Valor p
En estos resultados, la hipótesis nula indica que el costo de energía medio es igual a 200. Puesto que el valor p es 0.00, que es menor que el nivel de significancia de 0.05, usted puede rechazar la hipótesis nula y concluir que el costo medio de la población es diferente de 200.
Paso 3: Verificar si hay problemas en sus datos
Problemas con sus datos, como asimetría y valores atípicos, pueden afectar negativamente sus resultados. Utilice gráficas para buscar asimetría e identificar posibles valores atípicos.
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos.
Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Frecuentemente, es más fácil detectar la asimetría con un histograma o gráfica de caja.
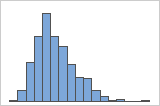
Asimétrico hacia la derecha
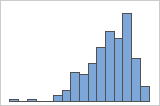
Asimétrico hacia la izquierda
El histograma con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos tiempos de espera son largos. El histograma con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos más fallan posteriormente.
Datos marcadamente asimétricos pueden afectar la validez del valor p si su muestra es pequeña (menos de 20 valores). Si sus datos son marcadamente asimétricos y tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
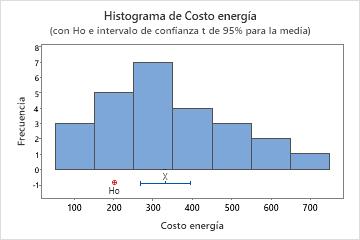
En este histograma, los datos no parecen ser muy asimétricos.
Identifique valores atípicos
Los valores atípicos, que son valores de datos que están muy alejados de otros valores de datos, pueden afectar fuertemente los resultados de su análisis. Frecuentemente, es más fácil identificar los valores atípicos en una gráfica de caja.
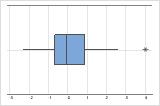
En una gráfica de caja, los asteriscos (*) denotan valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
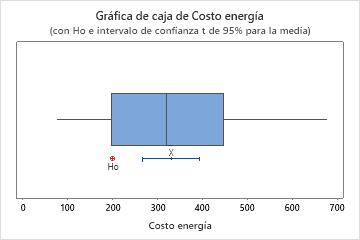
En esta gráfica de caja no hay valores atípicos.
