En este tema
Estadísticos
| Término | Description |
|---|---|
| tasa de ocurrencia |
 |
| ocurrencia media |
 |
La tasa es igual al número promedio de ocurrencias por unidad de longitud de observación. La media es el número promedio de ocurrencias en toda la muestra. Si la longitud es igual a 1, entonces la tasa y la media son iguales.
Valor p para la prueba exacta
Fórmula
- H1: λ > λ0: valor p = P(S ≥ s | λ = λ0) donde S tiene una distribución de Poisson con media nλ0t.
- H1: λ < λ0: valor p = P(S ≤ s | λ = λ0) donde S tiene una distribución de Poisson con media nλ0t.
- H1: λ ≠ λ0: Minitab utiliza una prueba de relación de verosimilitud de la siguiente manera:
Defina la función G(s), que expresa la prueba de relación de verosimilitud en términos de s, el número total de ocurrencias en el proceso de Poisson:

- si 0 ≤ s < nλ0t, resuelva la ecuación G(y) = G(s) para y en el intervalo (nλ0t, enλ0t];
valor p = P(S ≤ s | λ = λ0) + P(S ≥ y | λ = λ0)
- si s = nλ0t, entonces
valor p = 1.00
- si nλ0t < s ≤ enλ0t, resuelva la ecuación G(y) = G(s) para y en el intervalo [0, nλ0t);
valor p = P(S ≤ y | λ = λ0) + P(S ≥ s | λ = λ0)
- si s > enλ0t, la prueba es unilateral y
valor p = P(S ≥ s | λ = λ0)
donde S tiene una distribución de Poisson con media nλ0t.
- si 0 ≤ s < nλ0t, resuelva la ecuación G(y) = G(s) para y en el intervalo (nλ0t, enλ0t];
Notación
| Término | Description |
|---|---|
| s | número total de ocurrencias en el proceso de Poisson |
| t | "longitud" de la observación |
| λ0 | valor hipotético del parámetro de la tasa de la población |
| λ | valor real del parámetro de la tasa de la población |
| n | tamaño de la muestra |
| e | 2.71828, aproximadamente |
Intervalos de confianza y límites de confianza para la prueba exacta
Intervalos de confianza
Un intervalo de confianza exacto de 100(1 – α)% para la tasa de ocurrencia de un proceso de Poisson viene dado por:
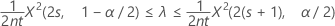

Límites de confianza
Cuando usted especifica una prueba unilateral, Minitab calcula un límite de confianza unilateral de 100(1 – α)%, de acuerdo con la dirección de la hipótesis alternativa.
-
Si usted especifica una hipótesis alternativa del tipo "mayor que", el límite inferior exacto de 100(1 – α)% de la tasa viene dado por:
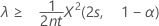
El límite inferior exacto de 100(1 – α)% de la media viene dado por:
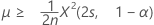
-
Si usted especifica una hipótesis alternativa del tipo "menor que", el límite superior exacto de 100(1 – α)% de la tasa viene dado por:
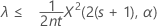
El límite superior exacto de 100(1 – α)% de la media viene dado por:
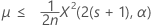
Notación
| Término | Description |
|---|---|
| s | número total de ocurrencias en el proceso de Poisson |
| t | "longitud" de la observación |
| λ | valor real de la tasa de la población |
| μ | valor real de la media de la población |
| Χ2(p, x) | punto percentil x superior de la distribución Χ2 con p grados de libertad, donde 0 < x < 1. |
| α | nivel de significancia para el intervalo de confianza de 100(1 – α)% |
| n | tamaño de la muestra |
Valor p para la aproximación a la normal
Las aproximaciones a la normal son válidas si el número total de ocurrencias es mayor que 10.
Fórmula
La prueba de hipótesis basada en una aproximación a la normal para Tasa de Poisson para 1 muestra utiliza las siguientes ecuaciones del valor p para las hipótesis alternativas respectivas:



Notación
| Término | Description |
|---|---|
| Z | 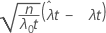 |
| t | "longitud" de la observación |
| λ 0 | valor hipotético del parámetro de la tasa de la población |
| λ | valor real del parámetro de la tasa de la población |
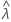 | valor observado del estadístico de la tasa de la muestra |
| n | tamaño de la muestra |
Intervalos de confianza y límites de confianza para la aproximación a la normal
Intervalos de confianza
Un intervalo de confianza de 100(1 – α)%, basado en una aproximación a la normal, para la tasa de ocurrencia de un proceso de Poisson viene dado por:
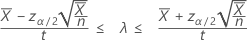
Cuando usted especifica un valor de "longitud", Minitab también muestra un intervalo de confianza para el número medio de ocurrencias. Ese intervalo de confianza viene dado por:
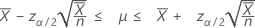
Límites de confianza
Cuando usted especifica una prueba unilateral, Minitab calcula un límite de confianza unilateral de 100(1 – α)%, de acuerdo con la dirección de la hipótesis alternativa.-
Si usted especifica una hipótesis alternativa del tipo "mayor que", el límite inferior exacto de 100(1 – α)% de la tasa viene dado por:
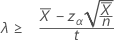
Si usted especifica un valor de "longitud", el límite inferior exacto de 100(1-α)% de la media viene dado por:
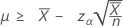
-
Si usted especifica una hipótesis alternativa del tipo "menor que", el límite superior exacto de 100(1 – α)% de la tasa viene dado por:
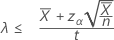
Si usted especifica un valor de "longitud", el límite superior exacto de 100(1 – α)% de la media viene dado por:
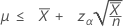
Notación
| Término | Description |
|---|---|
| s | número total de ocurrencias en el proceso de Poisson |
| t | "longitud" de la observación |
| λ | valor real de la tasa de la población |
| μ | valor real de la media de la población |
| Zx | punto percentil superior x de la distribución normal estándar, donde 0 < x < 1. |
| α | nivel de significancia para el intervalo de confianza de 100(1 – α)% |
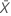 | número medio de ocurrencias en la muestra |
| n | tamaño de la muestra |
