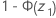En este tema
- Se ajustó el intervalo de confianza exacto de Blaker y los métodos de prueba
- Método del intervalo de confianza exacto de Clopper-Pearson
- Prueba que corresponde al intervalo de confianza exacto de Clopper-Pearson
- Método del intervalo de confianza de la puntuación de Wilson
- Prueba de puntuación
- Intervalo de confianza de Agresti-Coull y métodos de prueba
- Intervalo de confianza para la aproximación normal de Wald (aplicación web)
Se ajustó el intervalo de confianza exacto de Blaker y los métodos de prueba
La configuración de análisis para la hipótesis alternativa especifica si se debe producir un intervalo de confianza bilateral o un límite de confianza unilateral. Para una hipótesis alternativa de menor o mayor que, el análisis produce un límite de confianza unilateral. Para un límite de confianza unilateral, el análisis utiliza el método exacto de Clopper-Pearson.
Para una hipótesis alternativa bilateral, el análisis produce un intervalo de confianza bilateral. El análisis en Minitab Statistical Software produce el intervalo de confianza y el valor p utilizando el algoritmo de Klaschka y Reiczigel.1 El nombre de este método es el método exacto de Blaker ajustado. Este algoritmo numérico es más rápido de calcular y produce intervalos de confianza y pruebas que concuerdan en general. Los intervalos de confianza de Blaker ajustados también son exactos y anidados.
El método exacto de Blaker ajustado produce intervalos de confianza bilaterales para la proporción de eventos y produce valores de p para la hipótesis alternativa de p ≠ p0. Blaker23 proporciona un intervalo de confianza exacto de dos lados invirtiendo la función de valor p de una prueba exacta. Los intervalos de Clopper-Pearson son más amplios y siempre contienen los intervalos de confianza de Blaker. Los intervalos del método exacto de Blaker están anidados. Esta propiedad significa que los intervalos de confianza con niveles de confianza más altos contienen intervalos de confianza con niveles de confianza más bajos. Por ejemplo, un intervalo de confianza exacto de Blaker del 95% bilateral contiene el intervalo de confianza del 90% correspondiente.
El algoritmo que utiliza Minitab Statistical Software supera 2 limitaciones del método exacto original de Blaker. Una limitación es que el algoritmo numérico para calcular los intervalos de confianza es lento, especialmente cuando el tamaño de la muestra es grande. Otra limitación es que, para algunos datos, el método exacto original de Blaker produce un intervalo que cubre una proporción hipotética cuando el valor p es menor que el nivel de significación que corresponde al nivel de confianza. La limitación también surge cuando el intervalo de confianza no contiene una proporción hipotética cuando el valor p es mayor que el nivel de significación que corresponde al nivel de confianza.
Método del intervalo de confianza exacto de Clopper-Pearson
El intervalo (PL, PU) es un intervalo de confianza de 100(1 – α)% de p. Cuando la muestra no tiene eventos, el límite inferior es 0. Cuando el ejemplo solo tiene eventos, el límite superior es 1.
Límite inferior bilateral
Fórmula
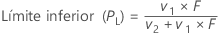
Notación
| Término | Description |
|---|---|
| v1 | 2x |
| v2 | 2(n – x + 1) |
| x | número de eventos |
| n | número de ensayos |
| F | punto α/2 inferior de la distribución F con v1 y v2 grados de libertad |
Límite superior bilateral
Fórmula

Notación
| Término | Description |
|---|---|
| v1 | 2(x + 1) |
| v2 | 2(n – x) |
| x | número de eventos |
| n | número de ensayos |
| F | punto α/2 superior de la distribución F con v1 y v2 grados de libertad |
Límite inferior unilateral
Fórmula

Notación
| Term | Description |
|---|---|
B(1 −  ; a, b) ; a, b) | percentil inferior a 1 -  de la distribución beta con parámetros a y b de la distribución beta con parámetros a y b |
| x | número de eventos |
| n | número de ensayos |
Límite superior unilateral
Fórmula

Notación
| Term | Description |
|---|---|
B( ; a, b) ; a, b) | percentil superior a  de la distribución beta con parámetros a y b de la distribución beta con parámetros a y b |
| x | número de eventos |
| n | número de ensayos |
Prueba que corresponde al intervalo de confianza exacto de Clopper-Pearson
Fórmula
- Ha: p ≠ p0
- Valor p =
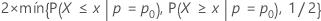
- Ha: p > p0
- p-valor = P{ X ≥ x | p = po}
- Ha: p < p0
- p-valor = P{ X ≤ x | p = po}
Notación
| Término | Description |
|---|---|
| p0 | proporción hipotética |
| n | número de ensayos |
| p | probabilidad de un evento |
| x | número de eventos |
Método del intervalo de confianza de la puntuación de Wilson
Wilson4 invierte la prueba de puntuación para obtener los intervalos de confianza que Minitab Statistical Software denomina intervalos de confianza de puntuación de Wilson. Los intervalos de puntuación de Wilson tienen dos formas, una sin corrección de continuidad y otra con corrección de continuidad. La cobertura de los intervalos sin la corrección está a veces por debajo del nivel de confianza nominal. El nivel de confianza real de los intervalos con la corrección es al menos el nivel de confianza nominal. Para ambos métodos, cuando la muestra no tiene eventos, el límite inferior es 0. Cuando el ejemplo solo tiene eventos, el límite superior es 1.
Intervalos sin corrección de continuidad
El intervalo de confianza bilateral del 100(1 – α)% tiene la siguiente fórmula:
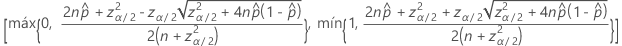
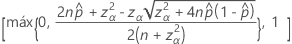
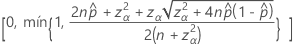
Intervalos con la corrección de continuidad
El límite inferior del intervalo bilateral del 100(1 – α)% tiene la siguiente fórmula:
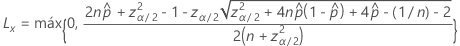
El límite superior del intervalo de dos lados del 100(1 – α)% tiene la siguiente fórmula:
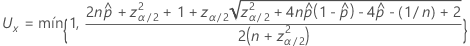
El límite inferior unilateral del 100(1 – α)% tiene la siguiente fórmula:
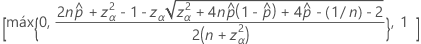
El límite superior unilateral del 100(1 – α)% tiene la siguiente fórmula:
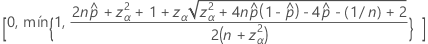
Notación
| Término | Description |
|---|---|
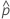 | probabilidad observada, 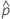 = x / n = x / n |
| x | número de eventos |
| n | número de ensayos |
| zγ | el punto percentil superior de la distribución normal estándar en γ |
| α | 1 – nivel de confianza/100 |
Prueba de puntuación
Método sin la corrección de continuidad
La prueba que corresponde al intervalo de confianza de la puntuación de Wilson y al método de aproximación normal (aplicación web) es la conocida prueba de puntuación. El estadístico de la prueba de puntuación tiene la siguiente ecuación:
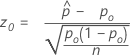
- Ha: p ≠ p0
- Valor p =
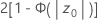
- Ha: p > p0
- Valor p =

- Ha: p < p0
- Valor p =

Método con la corrección de continuidad
El estadístico de prueba y el valor p para el procedimiento con corrección de continuidad dependen de la hipótesis alternativa.
- Ha: p ≠ p0
-
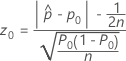
- Ha: p > p0
-
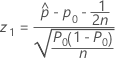
- Ha: p < p0
-
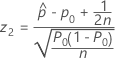
Notación
| Término | Description |
|---|---|
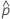 | probabilidad observada, x/n |
| x | número de eventos |
| n | número de ensayos |
| p0 | proporción hipotética |
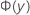 | función de distribución acumulativa de la distribución normal estándar en y |
Intervalo de confianza de Agresti-Coull y métodos de prueba
Intervalo de confianza
Agresti y Coull5 proporcionan un ajuste al método de Wald para intervalos de confianza que mejora las propiedades de cobertura. Para un intervalo de confianza bilateral del 95%, el ajuste suma aproximadamente 2 eventos y 2 no eventos y, a continuación, calcula los intervalos de confianza a partir de las fórmulas para las fórmulas del intervalo de confianza de Wald. Cuando la muestra no tiene eventos, el límite inferior es 0. Cuando el ejemplo solo tiene eventos, el límite superior es 1.
El intervalo de dos lados, 100(1 – α)% tiene la siguiente fórmula:
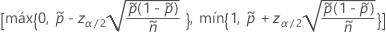
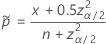
y
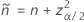
El límite inferior unilateral del 100(1 – α)% tiene la siguiente fórmula:
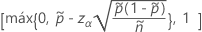
El límite superior unilateral del 100(1 – α)% tiene la siguiente fórmula:
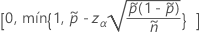
Para los límites unilaterales, use  En la definición de
En la definición de 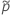 y
y 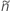 :
:
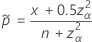
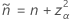
Prueba que corresponde al intervalo de Agresti-Coull
El análisis calcula el valor p de la prueba invirtiendo el procedimiento del intervalo de confianza.
Notación
| Término | Description |
|---|---|
| x | número de eventos |
| n | número de ensayos |
| zγ | el punto percentil superior de la distribución normal estándar en γ |
| α | 1 – nivel de confianza/100 |
Intervalo de confianza para la aproximación normal de Wald (aplicación web)
Fórmula
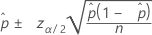
Notación
| Término | Description |
|---|---|
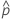 | probabilidad observada, 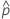 = x / n = x / n |
| x | número de eventos observados en n ensayos |
| n | número de ensayos |
| zα/2 | probabilidad acumulada inversa de la distribución normal estándar en 1–α/2 |
| α | 1 – nivel de confianza/100 |