En este tema
Intervalo de confianza
El rango en el que se espera que se encuentre la respuesta media estimada para un conjunto dado de valores de predictor.
Fórmula
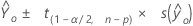
Notación
| Término | Description |
|---|---|
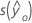 |  |
 | valor de respuesta ajustado para un conjunto dado de valores de predictor |
| α | tasa de error de tipo I |
| n | número de observaciones |
| p | número de parámetros del modelo |
| S 2(b) | matriz de varianzas-covarianzas de los coeficientes |
| s 2 | cuadrado medio del error |
| X | matriz de diseño |
| X0 | vector de valores dados de predictor con 1 columna y p filas |
| X'0 | transposición del nuevo vector de valores de predictor con 1 fila y p columnas |
Ajuste
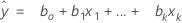
Notación
| Término | Description |
|---|---|
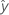 | valor ajustado |
| xk | késimo término. Cada término puede ser un solo predictor, un término polinómico o un término de interacción. |
| k | estimación del késimo coeficiente de regresión |
Error estándar del valor ajustado (EE ajuste)
El error estándar del valor ajustado en un modelo de regresión con un predictor es:

El error estándar del valor ajustado en un modelo de regresión con más de un predictor es:

Para la regresión ponderada, incluya la matriz de peso en la ecuación:

Cuando los datos tienen un conjunto de datos de prueba o una validación cruzada k-fold, las fórmulas son las mismas. El valor de s2 es de los datos de entrenamiento. La matriz de diseño y la matriz de peso también provienen de los datos de entrenamiento.
Notación
| Término | Description |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | i-ésimo predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| x'0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
Ecuación de regresión
Para un modelo con múltiples predictores, la ecuación es:
y = β0 + β1x1 + … + βkxk + ε
La ecuación ajustada es:
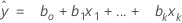
En la regresión lineal simple, que incluye solo un predictor, el modelo es:
y=ß0+ ß1x1+ε
Utilizando las estimaciones de regresión b0 para ß0 y b1 para ß1, el ecuación ajustada es:
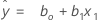
Notación
| Término | Description |
|---|---|
| y | respuesta |
| xk | késimo término. Cada término puede ser un solo predictor, un término polinómico o un término de interacción. |
| ßk | késimo coeficiente de regresión de la población |
| ε | término de error que sigue una distribución normal con una media de 0 |
| k | estimación del késimo coeficiente de regresión de la población |
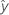 | respuesta ajustada |
Intervalo de predicción
El intervalo de predicción es el rango en el que se espera que se encuentre la respuesta ajustada para una nueva observación.
Fórmula
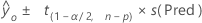
Notación
| Término | Description |
|---|---|
| s(Pred) |  |
 | valor de respuesta ajustado para un conjunto dado de valores predictores |
| α | nivel de significancia |
| n | número de observaciones |
| p | número de parámetros del modelo |
| s 2 | cuadrado medio del error |
| X | matriz de predictores |
| X0 | vector de valores dados de predictor con 1 columna y p filas |
| X'0 | transposición del nuevo vector de valores de predictor con 1 fila y p columnas |
