En este tema
Tabla Información de agrupación para múltiples comparaciones en parejas
Minitab utiliza los resultados del intervalo de confianza para la diferencia entre dos medias de nivel para obtener la información de agrupación. La información de agrupación se encuentra en una matriz. Suponga que un término tiene niveles K, entonces la dimensión máxima de la matriz es de k x k. Si todos los niveles están en un grupo, entonces la dimensión es de k x 1, con una letra "A" para todos los niveles de factor. Si todos los niveles están en grupos diferentes, la dimensión es de k x k con letras en la diagonal solamente.
- Ordene todas las medias de mínimos cuadrados a niveles diferentes de un término en orden descendiente, designado como 1, 2, ... , k.
- Defina una matriz a k x k con valor 0 en cada celda donde k = el número de niveles de factor.
- Para la columna j, donde j = 1, ... , Minitab realiza lo siguiente:
- Revise los intervalos de confianza de media j – media r, donde r = j + 1, .. , k. Si el intervalo para r contiene 0, establezca la résima fila y la jésima celda de columna, j) como 1.
- Establezca la celda (j, j) como 1 si al menos una celda en la columna j tiene un valor de 1.
- Calcule las sumas de la fila desde la columna 1 hasta la columna j para la fila l = j + 1, ... , k. Si el mínimo (todas las sumas de la fila) >= 1, se termina el bucle; de lo contrario se incrementa j en 1 y va al paso a.
- Para cada fila i, Minitab revisa la suma de todos los valores de columna para la fila ≥ 1. Si la suma es cero, establezca la celda de la fila i y la columna j = 1, donde la columna j es la primera fila en la matriz con valores de 0. Este procedimiento genera una matriz con valores de 1 y 0. El número total de grupos es el número de columnas con valor diferente a cero.
- Minitab coincide las letras con las columnas (por ejemplo A a la columna 1, B a la columna 2, etc.) y asigna a las celdas con el valor de 1 la letra correcta.
Tabla de información de agrupación para múltiples cmparaciones con un control
Minitab usa los resultados del intervalo de confianza para la diferencia entre cada media de nivel para obtener la información de agrupación. La información de agrupación se encuentra en una matriz con una columna.
Minitab asigna la letra "A" al nivel de control.
Si un intervalo contiene 0, entonces la media de nivel está en el mismo grupo que el nivel de control. Minitab asigna la letra "A" a la media de nivel.
Si un intervalo no contiene cero, entonces no se asigna ninguna letra.
Método de Tukey
Fórmula
Método de Tukey está disponible para todas las comparaciones en parejas. La fórmula para los intervalos de confianza es:
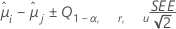
La fórmula para el estadístico de prueba es:


Para obtener detalles sobre el cálculo del valor p ajustado, consulte las referencias que se indican abajo.
Para encontrar la tasa de error individual a partir de la tasa de error simultánea, utilice la fórmula siguiente:
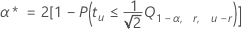
Notación
| Término | Description |
|---|---|
 | la media de mínimos cuadrados para el iésimo nivel de factor o combinación de niveles de factor |
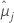 | la media de mínimos cuadrados para el jésimo nivel de factor o combinación de niveles de factor |
| r | el número de medias |
| Q1 − α, r, u | el percentil 1 − α de la distribución de rangos studentizados para r medias que se compararán con u grados de libertad |
| u | los grados de libertad para el error del modelo |
| SEE | el error estándar de la diferencia estimada entre las medias de los mínimos cuadrados |
| α | la probabilidad simultánea de cometer un error Tipo I, con base en la distribución de rangos studentizados |
| α* | la probabilidad individual de cometer un error Tipo I, con base en la distribución t para una comparación |
Referencias
1 Braun, H. I., editor (1994). The collected works of John W. Tukey: Volume VIII Multiple comparisons 1948-1983. New York: Chapman and Hall.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
Método de Fisher
Fórmula
Minitab ofrece diferentes métodos de intervalo de confianza para comparar las medias de los tratamientos. Para el método de Fisher, las cotas del intervalo de confianza y los valores p son iguales independientemente de si las comparaciones son en parejas o con un control. El método de Fisher utiliza el nivel de confianza individual. La fórmula para los intervalos de confianza es:
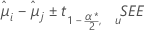
La fórmula para el estadístico de prueba es:

El valor p = 2*P{ T u > tu}
Para encontrar el nivel de confianza simultáneo a partir de la tasa de error individual, utilice la fórmula siguiente:

Notación
| Término | Description |
|---|---|
 | la media de mínimos cuadrados para el iésimo nivel de factor o combinación de niveles de factor |
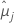 | la media de mínimos cuadrados para el jésimo nivel de factor o combinación de niveles de factor |
| t1-α*/2, u | el percentil superior α*/2 de la distribución t de Student con u grados de libertad |
| Tu | Variable aleatoria con una distribución T que tiene u grados de libertad para el error |
| Q | variable aleatoria con una distribución de rangos studentizados |
| α | la probabilidad simultánea de cometer un error de tipo I |
| α* | la probabilidad individual de cometer un error de tipo I |
| u | los grados de libertad para el error del modelo |
| SEE | el error estándar de la diferencia estimada entre las medias de los mínimos cuadrados |
Método de Bonferroni
Fórmula
Minitab ofrece diferentes métodos de intervalo de confianza para comparar las medias de los tratamientos. Puesto que el método de Bonferroni no establece ningún supuesto sobre la dependencia entre las comparaciones, es el método más conservador. "Conservador" en este contexto indica que es probable que el nivel de confianza real sea mayor que el nivel de confianza que se muestra. La fórmula para los intervalos de confianza es:
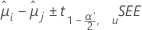
La fórmula para el estadístico de prueba es:

Notación
| Término | Description |
|---|---|
 | la media de mínimos cuadrados para el iésimo nivel de factor o combinación de niveles de factor |
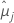 | la media de mínimos cuadrados para el jésimo nivel de factor o combinación de niveles de factor |
| t1-α*/2, u | el percentil superior α' /2 de la distribución t de Student con u grados de libertad |
| α | la probabilidad simultánea de cometer un error de tipo I |
| α' | α / c |
| c | el número de comparaciones |
| u | los grados de libertad para el error del modelo |
| SEE | el error estándar de la diferencia estimada entre las medias de los mínimos cuadrados |
El número de comparaciones depende de si las comparaciones son en parejas o con un control. Sea k el número de medias que se están comparando. El número de comparaciones se incluye en la siguiente tabla.
| En parejas | k (k – 1) / 2 |
| Con un control | k – 1 |
Método de Sidak
Fórmula
Minitab ofrece diferentes métodos de intervalo de confianza para comparar las medias de los tratamientos. El método de Sidak trata las comparaciones como si fueran independientes, lo que produce una aproximación conservadora de la tasa de error real. El método de Sidak es ligeramente más potente que el método de Bonferroni.
La fórmula para los intervalos de confianza es:
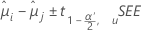
La fórmula para el estadístico de prueba es:

El valor p ajustado = 1 − (1 − p)c.
Notación
| Término | Description |
|---|---|
 | la media de mínimos cuadrados para el iésimo nivel de factor o combinación de niveles de factor |
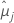 | la media de mínimos cuadrados para el jésimo nivel de factor o combinación de niveles de factor |
| t1-α*/2, u | el percentil superior α' /2 de la distribución t de Student con u grados de libertad |
| α | la probabilidad simultánea de cometer un error de tipo I |
| α' | 1 – (1 – α ) 1/ k |
| u | los grados de libertad para el error del modelo |
| SEE | el error estándar de la diferencia estimada entre las medias de los mínimos cuadrados |
| p | El valor p sin ajustar de la distribución t para una comparación |
| c | el número de comparaciones |
El número de comparaciones depende de si las comparaciones son en parejas o con un control. Sea k el número de combinaciones de factores. El número de comparaciones se incluye en la siguiente tabla.
| En parejas | k (k – 1) / 2 |
| Con un control | k – 1 |
Método de Dunnett
Fórmula
Minitab ofrece diferentes métodos de intervalo de confianza para comparar las medias de los tratamientos. El método de Dunnet está disponible para comparaciones con un control. La fórmula para los intervalos de confianza es:

La fórmula para el estadístico de prueba es:

El valor p ajustado es el resultado de la integración de la distribución que Dunnet propone para el estadístico de prueba. Para obtener detalles, consulte las referencias que se indican abajo.
Notación
| Término | Description |
|---|---|
 | la media de mínimos cuadrados para el iésimo nivel de factor o combinación de niveles de factor |
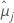 | la media de mínimos cuadrados para el jésimo nivel de factor o combinación de niveles de factor |
| D1-α, k-1, u | el percentil superior α de la distribución que Dunnett propone con k − 1 comparaciones y u grados de libertad |
| α | la probabilidad simultánea de cometer un error de tipo I |
| k | el número de medias que se compararán |
| u | los grados de libertad para el error del modelo |
| SEE | el error estándar de la diferencia estimada entre las medias de los mínimos cuadrados |
Referencias
1 Dunnett, C. W. (January 01, 1955). A multiple comparison procedure for comparing several treatments with a control. Journal of the American Statistical Association, 50, 1096-1121.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
