En este tema
N
El tamaño de la muestra (N) es el número total de observaciones en cada grupo.
Interpretación
El tamaño de la muestra afecta el intervalo de confianza y la potencia de la prueba.
Generalmente, una muestra más grande produce un intervalo de confianza más estrecho. Con un tamaño de muestra más grande, la prueba también tendrá más potencia para detectar una diferencia.
Media
La media de las observaciones dentro de cada grupo. La media describe cada grupo con un valor simple que identifique el centro de los datos. Es la suma de todas las observaciones con un grupo dividida entre el número de observaciones en ese grupo.
Interpretación
La media de cada muestra proporciona una estimación de la media de cada población. Las diferencias entre las medias de muestra son las estimaciones de las diferencias entre las medias de población.
Debido a que cada diferencia en las medias de los grupos se basa en los datos de una muestra y no de toda la población, usted no puede estar seguro de que sea igual a la diferencia en las poblaciones. Para obtener un mejor sentido de la diferencia poblacional, puede utilizar el intervalo de confianza.
Agrupación
Use la tabla Información de agrupación para determinar rápidamente si la diferencia media entre cualquier par de grupos es estadísticamente significativa.
La columna Agrupación contiene letras que agrupan los niveles de factor. Los grupos que no comparten una letra tienen una diferencia media que es estadísticamente significativa.
Si la tabla identifica diferencias que son estadísticamente significativas, utilice los intervalos de confianza de las diferencias para determinar si las diferencias son significativas desde el punto de vista práctico.
Usted puede hacer un análisis de comparación múltiple para términos aleatorios para determinar qué niveles del término son significativamente diferentes de los otros niveles. Por ejemplo, si usted estudia la eficacia de un medicamento sobre una enfermedad en particular, el sujeto suele ser un factor aleatorio significativo. Puede usar comparaciones múltiples para determinar si el medicamento afectó a los sujetos específicos incluidos en el estudio de un modo diferente (tal vez hizo que uno de ellos se sintiera peor).
Interpretación
Agrupar información utilizando el método de Tukey y una confianza de 95%
| Pintura | N | Media | Agrupación | |
|---|---|---|---|---|
| Mezcla 4 | 6 | 18.07 | A | |
| Mezcla 1 | 6 | 14.73 | A | B |
| Mezcla 3 | 6 | 12.98 | A | B |
| Mezcla 2 | 6 | 8.57 | B | |
En estos resultados, la tabla muestra que el grupo A contiene las Mezclas 1, 3 y 4 y el grupo B contiene las Mezclas 1, 2 y 3. Las Mezclas 1 y 3 están en ambos grupos. Las diferencias entre las medias que comparten una letra no son estadísticamente significativas. Las Mezclas 2 y 4 no comparten una letra, lo que indica que la Mezcla 4 posee una media significativamente mayor que la Mezcla 2.
Pruebas individuales de Fisher para las diferencias de las medias
Use los intervalos de confianza individuales para identificar las diferencias estadísticamente significativas entre las medias de grupo, para determinar los posibles rangos de las diferencias y para determinar si las diferencias son significativas desde el punto de vista práctico. La tabla Pruebas individuales de Fisher muestra un conjunto de intervalos de confianza para la diferencia entre los pares de medias.
El nivel de confianza individual es el porcentaje de veces que un solo intervalo de confianza incluye la diferencia real entre un par de medias de grupo, cuando se repite el estudio. Los intervalos de confianza individuales solo están disponibles para el método de Fisher. Todos los otros métodos de comparación producen intervalos de confianza simultáneos.
Controlar el nivel de confianza individual es poco común, porque no se controla el nivel de confianza simultáneo, que suele incrementarse hasta niveles inaceptables. Si no se controlan los intervalos de confianza simultáneos, la probabilidad de que al menos un intervalo de confianza no contenga la diferencia real aumenta con el número de comparaciones.
El intervalo de confianza de la diferencia consta de las dos partes siguientes:
- Estimación de punto
- La estimación de punto es la diferencia entre un par de medias y se calcula a partir de los datos de la muestra. El intervalo de confianza se centra en este valor.
- Margen de error
- El margen de error define la amplitud del intervalo de confianza y es determinado por la variabilidad observada en la muestra y el nivel de confianza. Para calcular el límite superior del intervalo de confianza, el margen de error se suma a la estimación de punto. Para calcular el límite inferior del intervalo de confianza, el margen de error se resta de la estimación de punto.
Interpretación
Utilice los intervalos de confianza para evaluar las diferencias entre las medias de grupo.
Pruebas individuales de Fisher para diferencias de las medias
| Diferencia de niveles | Diferencia de las medias | EE de diferencia | IC de 95% | Valor T | Valor p ajustado |
|---|---|---|---|---|---|
| Mezcla 2 - Mezcla 1 | -6.17 | 2.28 | (-10.92, -1.41) | -2.70 | 0.014 |
| Mezcla 3 - Mezcla 1 | -1.75 | 2.28 | (-6.51, 3.01) | -0.77 | 0.452 |
| Mezcla 4 - Mezcla 1 | 3.33 | 2.28 | (-1.42, 8.09) | 1.46 | 0.159 |
| Mezcla 3 - Mezcla 2 | 4.42 | 2.28 | (-0.34, 9.17) | 1.94 | 0.067 |
| Mezcla 4 - Mezcla 2 | 9.50 | 2.28 | (4.74, 14.26) | 4.17 | 0.000 |
| Mezcla 4 - Mezcla 3 | 5.08 | 2.28 | (0.33, 9.84) | 2.23 | 0.037 |
- El intervalo de confianza para la diferencia entre las medias de las Mezclas 4 y 2 se extiende de 4,74 a 14,26. Este rango no incluye cero, lo que indica que la diferencia entre estas medias es estadísticamente significativa.
- El intervalo de confianza para la diferencia entre las medias de las Mezclas 2 y 1 se extiende de -10,92 a -1,41. Este rango no incluye cero, lo que indica que la diferencia entre estas medias es estadísticamente significativa.
- El intervalo de confianza para la diferencia entre las medias de las Mezclas 4 y 3 se extiende de 0,33 a 9,84. Este rango no incluye cero, lo que indica que la diferencia entre estas medias es estadísticamente significativa.
- Los intervalos de confianza de los demás pares de medias incluyen el cero, lo que indica que las diferencias no son estadísticamente significativas.
- El nivel de confianza individual de 95% indica que usted puede estar 95% seguro de que cada intervalo de confianza contiene la diferencia real de esa comparación específica. Sin embargo, el nivel de confianza simultáneo indica que usted solamente puede estar 80,83% seguro de que todos los intervalos contienen las diferencias reales.
Diferencia de medias
Este valor es la diferencia entre las medias de muestra de dos grupos.
Interpretación
Las diferencias entre las medias de muestra de los grupos son estimaciones de las diferencias entre las poblaciones de estos grupos.
Puesto que cada diferencia en las media se basa en una muestra de datos y no de toda la población, usted no puede estar seguro de que sea igual a la diferencia en las poblaciones. Para entender mejor las diferencias entre las medias poblacionales, use los intervalos de confianza.
EE de diferencia
El error estándar de la diferencia entre las medias (EE de diferencia) estima la variabilidad de la diferencia entre las medias de muestra que usted obtendría si tomara muestras repetidas de las mismas poblaciones.
Interpretación
Use el error estándar de la diferencia entre medias para determinar con qué precisión las diferencias entre las medias de muestra estiman las diferencias entre las medias de población. Un valor de error estándar inferior indica una estimación más precisa.
Minitab usa el error estándar de la diferencia para calcular los intervalos de confianza de las diferencias entre medias, que es un rango de valores que probablemente incluye las diferencias en la población.
GL
Los grados de libertad (GL) son la cantidad de información en los datos. Minitab utiliza los grados de libertad para calcular la prueba t para las diferencias en las medias. Minitab solo muestra los grados de libertad si usted realiza comparaciones para un modelo de efectos mixtos.
IC simultáneo de 95%
Utilice los intervalos de confianza simultáneos de la diferencia (IC de 95%) para identificar las diferencias en las medias que son estadísticamente significativas, para determinar los posibles rangos de las diferencias y para evaluar la significancia práctica de las diferencias. La tabla muestra un conjunto de intervalos de confianza para la diferencia entre los pares de medias. Los intervalos de confianza que no contienen el cero indican una diferencia en las medias que es estadísticamente significativa.
El nivel de confianza simultáneo es el porcentaje de veces que un conjunto de intervalos de confianza incluye las diferencias reales de todas las comparaciones de grupos si el estudio se repite múltiples veces.
Controlar los intervalos de confianza simultáneos es particularmente importante cuando usted realiza comparaciones múltiples. Si no se controlan los intervalos de confianza simultáneos, la probabilidad de que al menos un intervalo de confianza no contenga la diferencia real aumenta con el número de comparaciones.
Para obtener más información, vaya a Explicación de los niveles de confianza simultáneos e individuales en las comparaciones múltiples.
El intervalo de confianza de la diferencia consta de las dos partes siguientes:
- Estimación de punto
- La estimación de punto es la diferencia entre un par de medias y se calcula a partir de los datos de la muestra. El intervalo de confianza se centra en este valor.
- Margen de error
- El margen de error define la amplitud del intervalo de confianza y es determinado por la variabilidad observada en la muestra, el tamaño de la muestra y el nivel de confianza. Para calcular el límite superior del intervalo de confianza, el margen de error se suma a la estimación de punto. Para calcular el límite inferior del intervalo de confianza, el margen de error se resta de la estimación de punto. El margen se amplía a medida que aumenta el número de comparaciones para mantener el nivel simultáneo de confianza de que todos los intervalos de confianza contienen las diferencias de población reales.
Usted puede hacer un análisis de comparación múltiple para términos aleatorios para determinar qué niveles del término son significativamente diferentes de los otros niveles. Por ejemplo, si usted estudia la eficacia de un medicamento sobre una enfermedad en particular, el sujeto suele ser un factor aleatorio significativo. Puede usar comparaciones múltiples para determinar si el medicamento afectó a los sujetos específicos incluidos en el estudio de un modo diferente (tal vez hizo que uno de ellos se sintiera peor).
Interpretación
Utilice los intervalos de confianza para evaluar las diferencias entre las medias de grupo.
Pruebas simultáneas de Tukey para diferencias de las medias
| Diferencia de Sujeto niveles | Diferencia de medias | EE de diferencia | IC simultáneo de 95% | Valor T | Valor p ajustado |
|---|---|---|---|---|---|
| 2 - 1 | 0.6567 | 0.0664 | (0.4768, 0.8366) | 9.89 | 0.000 |
| 3 - 1 | 0.9633 | 0.0708 | (0.7715, 1.1551) | 13.60 | 0.000 |
| 4 - 1 | 0.6900 | 0.0750 | (0.4870, 0.8930) | 9.20 | 0.000 |
| 3 - 2 | 0.3067 | 0.0632 | (0.1356, 0.4777) | 4.86 | 0.000 |
| 4 - 2 | 0.0333 | 0.0678 | (-0.1502, 0.2169) | 0.49 | 0.960 |
| 4 - 3 | -0.2733 | 0.0721 | (-0.4686, -0.0781) | -3.79 | 0.003 |
- El intervalo de confianza para la diferencia entre las medias de los Sujetos 4 y 2 es de -0,1502 a 0,2169. Este rango incluye el cero, lo que indica que la diferencia no es estadísticamente significativa.
- Los intervalos de confianza de los demás pares de medias no incluyen el cero, lo que indica que esas diferencias son estadísticamente significativas.
- El nivel de confianza simultáneo de 95% indica que usted puede estar 95% seguro de que todos los intervalos de confianza contienen las diferencias reales.
- La tabla indica que el nivel de confianza individual es 98,94%. Este resultado indica que usted puede estar 98,94% seguro de que cada intervalo individual contiene la diferencia real entre un par específico de medias de grupo.
- El nivel de confianza individual de 98,94% para cada comparación produce colectivamente el nivel de confianza simultáneo de 95% para las seis comparaciones.
Valor t
El valor t es un estadístico de prueba que mide la relación entre la diferencia en las medias y el error estándar de la diferencia.
Interpretación
Usted puede utilizar el valor t para determinar si puede rechazar la hipótesis nula, que indica que la diferencia en las medias es 0. Sin embargo, la mayoría de las personas utiliza el valor p, porque es más fácil de interpretar. Para obtener más información sobre cómo usar el valor crítico, vaya a Uso del valor t para determinar si se puede rechazar la hipótesis nula.
Minitab utiliza el valor t para calcular el valor p.
Valor p ajustado
El valor p ajustado indica cuales pares dentro de una familia de comparaciones son significativamente diferentes. El ajuste limita la tasa de error por familia al nivel de significancia que usted especifique. Si usted utiliza un valor p regular para comparaciones múltiples, la tasa de error por familia aumenta con cada comparación adicional.
Es importante considerar la tasa de error por familia al realizar comparaciones múltiples, porque las probabilidades de cometer un error de tipo I para una serie de comparaciones son mayores que la tasa de error para una comparación individual.
Interpretación
Si el valor p ajustado es menor que alfa, rechace la hipótesis nula y concluya que la diferencia entre las medias de un par de grupo es estadísticamente significativa. El valor p ajustado también representa la menor tasa de error por familia en la cual se rechaza una hipótesis nula en particular.
Gráfica de intervalo para las diferencias de las medias
Utilice los intervalos de confianza para determinar los posibles rangos de las diferencias y para evaluar la significancia práctica de esas diferencias. La gráfica muestra un conjunto de intervalos de confianza para la diferencia entre los pares de medias. Los intervalos de confianza que no contienen el cero indican una diferencia en las medias que es estadísticamente significativa.
Dependiendo del método de comparación que elija, la gráfica compara diferentes pares de grupos y muestra uno de los siguientes tipos de intervalos de confianza.
-
Nivel de confianza individual
El porcentaje de veces que un solo intervalo de confianza incluiría la diferencia real entre un par de medias de grupo si el estudio se repitiera múltiples veces.
-
Nivel de confianza simultáneo
El porcentaje de veces que un conjunto de intervalos de confianza incluiría las diferencias reales de todas las comparaciones de grupos si el estudio se repitiera múltiples veces.
Controlar los intervalos de confianza simultáneos es particularmente importante cuando usted realiza comparaciones múltiples. Si no se controlan los intervalos de confianza simultáneos, la probabilidad de que al menos un intervalo de confianza no contenga la diferencia real aumenta con el número de comparaciones.
Para obtener más información, vaya a Explicación de los niveles de confianza simultáneos e individuales en las comparaciones múltiples.
Usted puede hacer un análisis de comparación múltiple para términos aleatorios para determinar qué niveles del término son significativamente diferentes de los otros niveles. Por ejemplo, si usted estudia la eficacia de un medicamento sobre una enfermedad en particular, el sujeto suele ser un factor aleatorio significativo. Puede usar comparaciones múltiples para determinar si el medicamento afectó a los sujetos específicos incluidos en el estudio de un modo diferente (tal vez hizo que uno de ellos se sintiera peor).
Interpretación
Utilice los intervalos de confianza para evaluar las diferencias entre las medias de grupo.
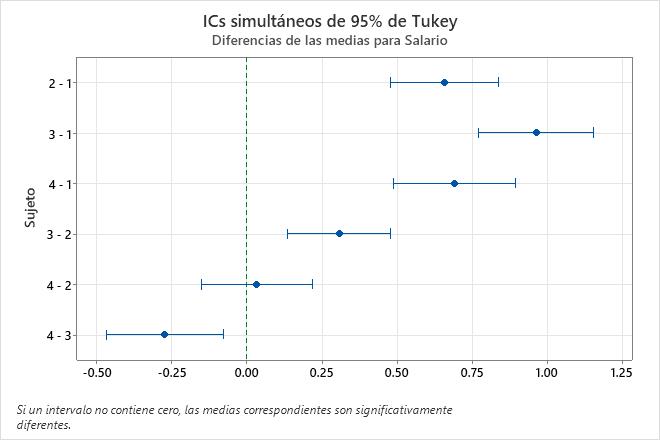
Pruebas simultáneas de Tukey para diferencias de las medias
| Diferencia de Sujeto niveles | Diferencia de medias | EE de diferencia | IC simultáneo de 95% | Valor T | Valor p ajustado |
|---|---|---|---|---|---|
| 2 - 1 | 0.6567 | 0.0664 | (0.4768, 0.8366) | 9.89 | 0.000 |
| 3 - 1 | 0.9633 | 0.0708 | (0.7715, 1.1551) | 13.60 | 0.000 |
| 4 - 1 | 0.6900 | 0.0750 | (0.4870, 0.8930) | 9.20 | 0.000 |
| 3 - 2 | 0.3067 | 0.0632 | (0.1356, 0.4777) | 4.86 | 0.000 |
| 4 - 2 | 0.0333 | 0.0678 | (-0.1502, 0.2169) | 0.49 | 0.960 |
| 4 - 3 | -0.2733 | 0.0721 | (-0.4686, -0.0781) | -3.79 | 0.003 |
- El intervalo de confianza para la diferencia entre las medias de los Sujetos 4 y 2 es de -0.1502 a 0.2169. Este rango incluye el cero, lo que indica que la diferencia no es estadísticamente significativa.
- Los intervalos de confianza de los demás pares de medias no incluyen el cero, lo que indica que esas diferencias son estadísticamente significativas.
- El nivel de confianza simultáneo de 95% indica que usted puede estar 95% seguro de que todos los intervalos de confianza contienen las diferencias reales.
- La tabla indica que el nivel de confianza individual es 98.94%. Este resultado indica que usted puede estar 98.94% seguro de que cada intervalo individual contiene la diferencia real entre un par específico de medias de grupo.
- El nivel de confianza individual de 98.94% para cada comparación produce colectivamente el nivel de confianza simultáneo de 95% para las seis comparaciones.
