Minitab ofrece varios análisis que permiten analizar las series de tiempo. Estos análisis incluyen los métodos simples de pronóstico y suavización, los métodos de análisis de correlaciones y el modelo ARIMA. Aunque el análisis de correlaciones puede realizarse separadamente del modelo ARIMA, Minitab presenta los métodos de correlación como parte del modelo ARIMA.
Métodos simples de pronóstico y suavización
Los métodos simples de pronóstico y suavización modelan los componentes de una serie que habitualmente se observa fácilmente en una gráfica de series de tiempo de los datos. Este enfoque descompone los datos en sus partes componentes y luego extiende las estimaciones de los componentes en el futuro para generar pronósticos. Usted puede elegir entre los métodos estáticos del análisis de tendencia y descomposición o los métodos dinámicos de promedio móvil, suavización exponencial individual y doble y el método de Winters. Los métodos estáticos tienen patrones que no cambian con el tiempo, los métodos dinámicos tienen patrones que sí cambian con el tiempo y las estimaciones se actualizan utilizando los valores contiguos.
Usted puede utilizar dos métodos combinados. Es decir, puede elegir un método estático para modelar un componente y un método dinámico para modelar otro componente. Por ejemplo, puede ajustar una tendencia estática usando un análisis de tendencia y modelar dinámicamente el componente estacional en los residuos usando el método de Winters. Alternativamente, puede ajustar un modelo estacional estático usando la descomposición y modelar dinámicamente el componente de tendencia en los residuos usando la suavización exponencial doble. Usted también puede aplicar un análisis de tendencia y descomposición juntos para poder usar la selección más amplia de modelos de tendencia ofrecidos por el análisis de tendencia. Una desventaja de la combinación de métodos es que los intervalos de confianza para los pronósticos no son válidos.
Para cada uno de los métodos, la siguiente tabla muestra un resumen y una gráfica de ajustes y pronósticos de datos comunes.
Análisis de tendencia
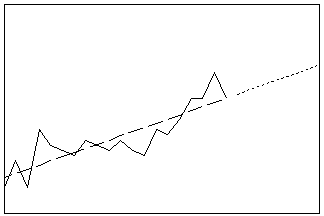
Ajusta un modelo de tendencia general a los datos de las series de tiempo. Elija entre los modelos de tendencia lineal, cuadrático, crecimiento o decadencia exponencial y curva S. Utilice este procedimiento para ajustar la tendencia cuando sus series no incluyan un componente estacional.
- Longitud: largo
- Perfil: extensión de la línea de tendencia
Descomposición
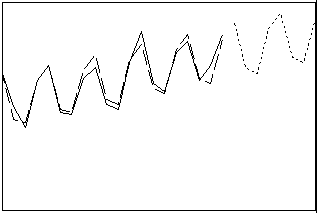
Separa las series de tiempo en componentes de tendencia lineal, componentes estacionales y el error. Elija si el componente estacional es aditivo o multiplicativo con la tendencia. Utilice este procedimiento para pronosticar cuando haya un componente estacional en sus series o cuando desee examinar la naturaleza de los componentes.
- Longitud: largo
- Perfil: tendencia con patrón estacional
Promedio móvil
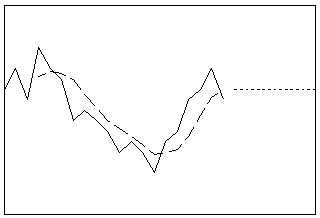
Suaviza los datos al promediar las observaciones consecutivas en una serie. Puede usar este procedimiento cuando los datos no tengan un componente de tendencia. Si tiene un componente estacional, establezca la longitud del promedio móvil igual a la longitud del ciclo estacional.
- Longitud: corto
- Perfil: línea plana
Suavización exponencial individual
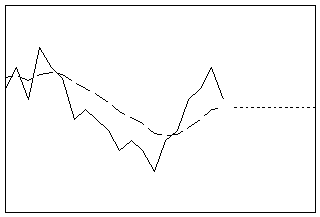
Suaviza los datos usando la fórmula de pronóstico de ARIMA óptimo (0,1,1) de un paso adelante. Este procedimiento funciona mejor sin un componente de tendencia o estacional. El componente dinámico individual en un modelo de promedio móvil es el nivel.
- Longitud: corto
- Perfil: línea plana
Suavización exponencial doble
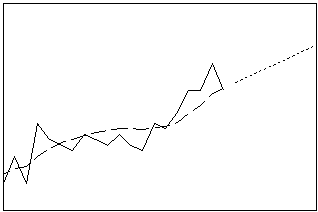
Suaviza los datos usando la fórmula de pronóstico de ARIMA óptimo (0,2,2) de un paso adelante. Este procedimiento puede funcionar adecuadamente cuando hay una tendencia, pero también puede servir como un método de suavización general. La suavización exponencial doble calcula las estimaciones dinámicas para dos componentes: nivel y tendencia.
- Longitud: corto
- Perfil: línea recta con pendiente igual a la última estimación de tendencia
Método de Winters
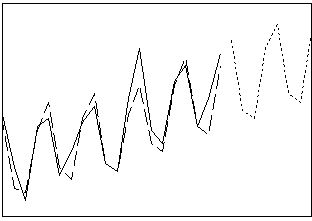
Suaviza los datos mediante la suavización exponencial de Holt-Winters. Utilice este procedimiento cuando haya tendencia y estacionalidad, siendo estos dos componentes o aditivos o multiplicativos. El Método de Winters calcula estimaciones dinámicas para tres componentes: nivel, tendencia y estacional.
- Longitud: de corta a mediana
- Perfil: tendencia con patrón estacional
Análisis de correlaciones y modelo ARIMA
El modelo ARIMA (promedio móvil integrado autorregresivo) también utiliza los patrones en los datos, pero estos patrones podrían no visualizarse fácilmente en una gráfica de los datos. En lugar de ello, el modelo ARIMA utiliza las funciones de diferenciación, autocorrelación y autocorrelación parcial para ayudar a identificar un modelo aceptable.
El modelo ARIMA puede utilizarse para modelar muchas series de tiempo diferentes, con o sin componentes de tendencia o estacionales y para generar pronósticos. El perfil del pronóstico depende del modelo que se ajusta. La ventaja del modelo ARIMA comparado con los métodos simples de pronóstico y suavización es que es más flexible para ajustarse a los datos. Sin embargo, la identificación y el ajuste de un modelo pueden consumir mucho tiempo y el modelo ARIMA no se automatiza con facilidad.
- Diferencias
- Calcula y almacena las diferencias entre los valores de los datos de una serie de tiempo. Si desea ajustar un modelo ARIMA, pero los datos tienen un componente de tendencia o estacionalidad, la diferenciación de los datos es un paso común para evaluar los modelos ARIMA probables. Las diferencias se utilizan para simplificar la estructura de correlaciones y para revelar cualquier patrón subyacente.
- Desfase
- Calcula y almacena los desfases de una serie de tiempo. Cuando usted aplica un desfase a una serie de tiempo, Minitab mueve los valores originales hacia abajo en la columna e inserta valores faltantes en la parte superior de la columna. El número de valores faltantes insertados depende de la longitud del desfase.
- Autocorrelación
- Calcula y crea una gráfica de las autocorrelaciones de una serie de tiempo. La autocorrelación es la correlación entre observaciones de una serie de tiempo separadas por k unidades de tiempo. La gráfica de las autocorrelaciones se denomina función de autocorrelación (ACF). Como guía para elegir los términos que incluirá en un modelo ARIMA, observe la ACF.
- Autocorrelación parcial
- Calcula y crea una gráfica de autocorrelaciones parciales de una serie de tiempo. Las autocorrelaciones parciales, al igual que las autocorrelaciones, son correlaciones entre conjuntos de pares de datos ordenados de una serie de tiempo. Como sucede con las correlaciones parciales en el caso de la regresión, las autocorrelaciones parciales miden la fuerza de la relación con otros términos que están siendo evaluados. La autocorrelación parcial en un desfase de k es la correlación entre los residuos en el tiempo t de un modelo autorregresivo y las observaciones en el desfase k con los términos para todos los desfases intermedios presentes en el modelo autorregresivo. La gráfica de autocorrelaciones parciales se denomina función de autocorrelación parcial (PACF). Como guía para elegir los términos que incluirá en un modelo ARIMA, observe la PACF.
- Intercorrelación
- Calcula y crea una gráfica de las correlaciones entre dos series de tiempo.
- ARIMA
- Ajusta un modelo ARIMA de Box-Jenkins a una serie de tiempo. En ARIMA, "autorregresivo", "integrado" y "promedio móvil" se refieren a los pasos de filtrado que se toman para calcular el modelo ARIMA hasta que solamente queda el ruido aleatorio. Utilice ARIMA para modelar el comportamiento de las series de tiempo y para generar pronósticos.
