En este tema
Multiplicativo
Fórmula
El modelo multiplicativo es:
- Lt = α (Yt / St–p) + (1 – α) [Lt–1 + Tt–1]
- Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
- St = δ (Yt / Lt) + (1 – δ) St–p
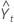 = (Lt–1 + Tt–1) St–p
= (Lt–1 + Tt–1) St–p
Notación
| Término | Description |
|---|---|
| Lt | el nivel en el tiempo t, α es la ponderación para el nivel |
| Tt | tendencia en el tiempo t, |
| γ | la ponderación para la tendencia |
| St | componente estacional en el tiempo t |
| δ | la ponderación para el componente estacional |
| p | período estacional |
| Yt | el valor de los datos en el tiempo t |
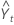 | el valor ajustado o el pronóstico de un periodo por anticipado, en el tiempo t |
Método para calcular los valores iniciales para nivel y tendencia en modelos multiplicativos.
El siguiente método supone una longitud estacional superior a 4.
- Busque la media, el valor mínimo y el máximo de los datos. Para este ejemplo:
- Media = 554.208
- Mín. = 1
- Máx. = 1498.47
- Para cada fila de datos, calcule:

- Donde N es igual a la longitud estacional. Para este ejemplo, N = 12.
- Ejecute la regresión utilizando los primeros "valores temporales" N (calculados en el paso 2) como variable Y y un vector de 1 a N como variable X. Por lo tanto, para este ejemplo:
Y X 4104.36 1 4104.36 2 4630.36 3 4922.80 4 4822.40 5 5601.83 6 4891.77 7 4604.44 8 4411.26 9 4123.66 10 4104.36 11 4104.36 12 La pendiente de la línea de regresión es el valor inicial de la tendencia.
- Ajuste la intersección para la línea de regresión por medio de una resta:

La intersección de sus datos es 4705.24. Reste 4103.36 de la intersección para obtener una intersección ajustada de 601.879. Esta intersección ajustada es el valor inicial para el nivel.
Aditivo
Fórmula
- Lt = α (Yt – St–p) + (1 – α) [Lt–1 + Tt–1]
- Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
- St = δ (Yt – Lt) + (1 – δ) St–p
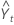 = Lt–1 + Tt–1 + St–p
= Lt–1 + Tt–1 + St–p
Notación
| Término | Description |
|---|---|
| Lt | el nivel en el tiempo t, α es la ponderación para el nivel |
| Tt | tendencia en el tiempo t, |
| γ | la ponderación para la tendencia |
| St | componente estacional en el tiempo t |
| δ | la ponderación para el componente estacional |
| p | período estacional |
| Yt | el valor de los datos en el tiempo t |
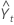 | el valor ajustado o el pronóstico de un periodo por anticipado, en el tiempo t |
Método para calcular los valores iniciales para nivel y tendencia en modelos aditivos.
El siguiente método supone una longitud estacional superior a 4.
- Donde N es igual a la longitud estacional. Para este ejemplo, N = 12.
- Ejecute la regresión utilizando los primeros valores de datos N como variable Y y un vector de 1 a N como variable X. Por lo tanto, para este ejemplo:
Y X 1.00 1 1.00 2 527.00 3 819.45 4 719.04 5 1498.47 6 788.42 7 501.08 8 307.90 9 20.30 10 1.00 11 1.00 12 La pendiente de la línea de regresión es el valor inicial de la tendencia. La intersección de la línea de regresión es el valor inicial para el nivel.
Método para calcular los valores iniciales de los índices estacionales para los modelos aditivos
El siguiente método supone una longitud estacional superior a 4.
- Ejecute la regresión utilizando los valores de datos como variable Y y un vector de 1 a 24 como variable X. Por lo tanto, para este ejemplo:
Y X 1.00 1 1.00 2 527.00 3 819.45 4 719.04 5 1498.47 6 788.42 7 501.08 8 307.90 9 20.30 10 1.00 11 1.00 12 83.00 13 668.21 14 1121.28 15 1386.84 16 1031.18 17 988.60 18 1380.30 19 1005.97 20 233.69 21 211.87 22 2.00 23 2.40 24 Utilice los residuos de este modelo de regresión en el siguiente paso
- Ejecute la regresión utilizando los residuos como variable Y y 12 variables indicadoras (z.1 a z.12) como variables X. Ajuste el modelo de regresión sin un término de intersección (constante). Por lo tanto, para este ejemplo:
Residuos z.1 z.2 z.3 z.4 z.5 z.6 z.7 z.8 z.9 z.10 z.11 z.12 -508.261 1 0 0 0 0 0 0 0 0 0 0 0 -512.170 0 1 0 0 0 0 0 0 0 0 0 0 9.926 0 0 1 0 0 0 0 0 0 0 0 0 298.460 0 0 0 1 0 0 0 0 0 0 0 0 194.145 0 0 0 0 1 0 0 0 0 0 0 0 969.667 0 0 0 0 0 1 0 0 0 0 0 0 255.705 0 0 0 0 0 0 1 0 0 0 0 0 -35.538 0 0 0 0 0 0 0 1 0 0 0 0 -232.625 0 0 0 0 0 0 0 0 1 0 0 0 -524.137 0 0 0 0 0 0 0 0 0 1 0 0 -547.346 0 0 0 0 0 0 0 0 0 0 1 0 -551.254 0 0 0 0 0 0 0 0 0 0 0 1 -473.161 1 0 0 0 0 0 0 0 0 0 0 0 108.141 0 1 0 0 0 0 0 0 0 0 0 0 557.303 0 0 1 0 0 0 0 0 0 0 0 0 818.952 0 0 0 1 0 0 0 0 0 0 0 0 459.378 0 0 0 0 1 0 0 0 0 0 0 0 412.890 0 0 0 0 0 1 0 0 0 0 0 0 800.684 0 0 0 0 0 0 1 0 0 0 0 0 422.451 0 0 0 0 0 0 0 1 0 0 0 0 -353.739 0 0 0 0 0 0 0 0 1 0 0 0 -379.468 0 0 0 0 0 0 0 0 0 1 0 0 -593.247 0 0 0 0 0 0 0 0 0 0 1 0 Los coeficientes de este modelo de regresión son los valores iniciales de los índices estacionales. Los coeficientes son:Punto COEF1 1 -490.711 2 -202.014 3 283.615 4 558.706 5 326.762 6 691.278 7 528.195 8 193.456 9 -293.182 10 -451.803 11 -570.297 12 -574.005 Nota
Las variables del indicador z.1 a z.12 indican a qué mes del período pertenece cada punto de datos. Por ejemplo, la variable z.1 es igual a 1 para el primer mes del período y es igual a 0 si no se trata del primer mes.
Ajuste del modelo
El método de Winters emplea un componente de nivel, un componente de tendencia y un componente estacional en cada período. Utiliza tres ponderaciones, o parámetros de suavización, para actualizar los componentes en cada período. Los valores iniciales para los componentes de nivel y de tendencia se obtienen de una regresión lineal sobre el tiempo. Los valores iniciales para el componente estacional se obtienen de una regresión de variables simulada utilizando datos sin tendencia.
Pronósticos
El método de Winters utiliza los componentes de nivel, tendencia y estacional para generar pronósticos. El método de Winters también utiliza datos hasta el tiempo de origen del pronóstico para generar los pronósticos.
Fórmula
- Método multiplicativo: (Lt + mTt) * St + m −p
- Método aditivo: Lt + mTt +St + m −p
Notación
| Término | Description |
|---|---|
| Lt | nivel |
| Tt | la tendencia en el tiempo t |
| Término | Description |
|---|---|
| St + m −p | componente estacional para el mismo período del año anterior |
Intervalos de predicción
Para cada pronóstico, el análisis produce un intervalo de predicción.
Fórmula
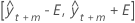
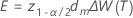
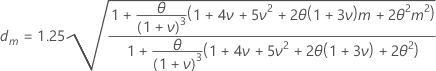
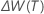 depende de si el modelo es aditivo o multiplicativo.
depende de si el modelo es aditivo o multiplicativo.- Aditivo
-
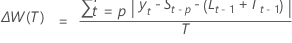
- Multiplicativo
-
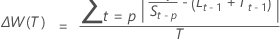
Notación
| Término | Description |
|---|---|
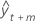 | El pronóstico en el tiempo t + m |
| t | El origen de las previsiones |
| m | el índice de pronóstico, por ejemplo, 1 para el primer pronóstico |
 |
la probabilidad acumulada inversa de la distribución normal estándar en 1- α /2; α = nivel de confianza/100 |
| θ | El máximo de las constantes de suavizado, alfa (nivel), gamma (tendencia) y delta (estacional) |
| ν | 1 – θ |
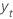 | el valor observado de la serie temporal en el tiempo t |
 | el componente estacional de un ciclo estacional completo antes del tiempo t |
 | el componente de nivel para el tiempo t – 1 |
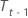 | El componente de tendencia para el tiempo t – 1 |
| T | el número de valores de datos de la serie en los que existen el componente estacional, el componente de nivel y el componente de tendencia |
MAPE
El error porcentual absoluto medio (EPAM) mide la exactitud de los valores ajustados de las series de tiempo. EPAM expresa la exactitud como un porcentaje.
Fórmula
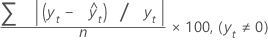
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
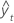 | valor ajustado |
| n | número de observaciones |
MAD
La desviación media absoluta (MAD) mide la exactitud de los valores ajustados de las series de tiempo. La MAD expresa exactitud en las mismas unidades que los datos, lo cual ayuda a conceptualizar la cantidad de error.
Fórmula
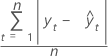
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
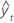 | valor ajustado |
| n | número de observaciones |
DCM
La desviación cuadrática media (DCM) siempre se calcula utilizando el mismo denominador, n, independientemente del modelo. La DCM es más sensible que DAM para medir un error de pronóstico inusualmente grande.
Fórmula
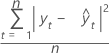
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
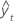 | valor ajustado |
| n | número de observaciones |
