En este tema
Longitud
El número de observaciones en las series de tiempo.
α (nivel)
α es la ponderación utilizada en el componente de nivel de la estimación suavizada. α es similar a un promedio móvil de las observaciones. Las ponderaciones ajustan el nivel de suavización al definir la reacción de cada componente ante las condiciones actuales. Las ponderaciones más bajas ofrecen menos ponderación a los datos recientes. Las ponderaciones más elevadas ofrecen más ponderación a los datos recientes. Ajustar la ponderación para el componente de nivel por lo general tiene la mejor probabilidad de mejorar las medidas de exactitud. Cambiar las demás ponderaciones por lo general tiene un efecto menor después de ajustar la ponderación de nivel donde debería estar.
γ (tendencia)
Las ponderaciones más elevadas ofrecen más influencia a los datos recientes, de modo que los pronósticos (en verde) siguen la tendencia descendente al final de los datos (en negro).
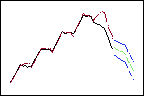
Mayor ponderación de tendencia
Las ponderaciones más bajas ofrecen menos influencia a los datos recientes, de modo que los pronósticos siguen la tendencia ascendente general.
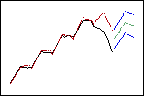
Menor ponderación de tendencia
δ (estacional)
δ es la ponderación utilizada en el componente estacional de la estimación suavizada. Las ponderaciones ajustan el nivel de suavización al definir la reacción de cada componente ante las condiciones actuales. Las ponderaciones más bajas ofrecen menos ponderación a los datos recientes. Las ponderaciones más elevadas ofrecen más ponderación a los datos recientes.
MAPE
El error porcentual absoluto medio (MAPE) expresa la exactitud como un porcentaje del error. Debido a que el MAPE es un porcentaje, puede ser más fácil de entender que otros estadísticos de medición de exactitud. Por ejemplo, si el MAPE es 5, en promedio, el pronóstico está errado en un 5%.
Sin embargo, es posible que algunas veces observe un valor de MAPE muy elevado aunque el modelo parezca ajustarse a los datos adecuadamente. Examine la gráfica para ver si los valores de los datos se aproximan a 0. Debido a que MAPE divide el error absoluto entre los datos reales, los valores que se aproximan a 0 pueden aumentar significativamente el MAPE.
Interpretación
Utilice para comparar los ajustes de diferentes modelos de series de tiempo. Valores más pequeños indican un mejor ajuste. Si un modelo individual no tiene los valores más bajos para las 3 medidas de exactitud, MAPE es generalmente la medición más recomendable.
Las medidas de exactitud se basan en residuos de un período por delante. En cada punto en el tiempo, se utiliza el modelo para predecir el valor Y correspondiente al siguiente período en el tiempo. La diferencia entre los valores pronosticados (ajustes) y Y real son los residuos un período por delante. Por tal motivo, las medidas de exactitud proporcionan un indicio de la exactitud que usted pudiera esperar al pronosticar 1 período proveniente del final de los datos. Por lo tanto, no indican la exactitud al pronosticar más de 1 período. Si está utilizando el modelo para realizar pronósticos, no debería basar su decisión únicamente en las medidas de exactitud. Usted también debería examinar el ajuste del modelo para garantizar que el modelo sigue los datos de manera estrecha, particularmente al final de las series.
MAD
La desviación absoluta de la media (MAD) expresa exactitud en las mismas unidades que los datos, lo que ayuda a conceptualizar la cantidad del error. Los valores atípicos tienen menos efecto en MAD que en MSD.
Interpretación
Utilice para comparar los ajustes de diferentes modelos de series de tiempo. Valores más pequeños indican un mejor ajuste.
Las medidas de exactitud se basan en residuos de un período por delante. En cada punto en el tiempo, se utiliza el modelo para predecir el valor Y correspondiente al siguiente período en el tiempo. La diferencia entre los valores pronosticados (ajustes) y Y real son los residuos un período por delante. Por tal motivo, las medidas de exactitud proporcionan un indicio de la exactitud que usted pudiera esperar al pronosticar 1 período proveniente del final de los datos. Por lo tanto, no indican la exactitud al pronosticar más de 1 período. Si está utilizando el modelo para realizar pronósticos, no debería basar su decisión únicamente en las medidas de exactitud. Usted también debería examinar el ajuste del modelo para garantizar que el modelo sigue los datos de manera estrecha, particularmente al final de las series.
MSD
La desviación cuadrática media (MSD) mide la exactitud de los valores ajustados de las series de tiempo.Los valores atípicos tienen mayor efecto en MSD que en MAD.
Interpretación
Utilice para comparar los ajustes de diferentes modelos de series de tiempo. Valores más pequeños indican un mejor ajuste.
Las medidas de exactitud se basan en residuos de un período por delante. En cada punto en el tiempo, se utiliza el modelo para predecir el valor Y correspondiente al siguiente período en el tiempo. La diferencia entre los valores pronosticados (ajustes) y Y real son los residuos un período por delante. Por tal motivo, las medidas de exactitud proporcionan un indicio de la exactitud que usted pudiera esperar al pronosticar 1 período proveniente del final de los datos. Por lo tanto, no indican la exactitud al pronosticar más de 1 período. Si está utilizando el modelo para realizar pronósticos, no debería basar su decisión únicamente en las medidas de exactitud. Usted también debería examinar el ajuste del modelo para garantizar que el modelo sigue los datos de manera estrecha, particularmente al final de las series.
Suavizar
Los datos suavizados son la suma del componente de nivel y el componente estacional (modelo aditivo) o el producto del componente de nivel y el componente estacional (modelo multiplicativo).
Predecir
Los valores pronosticados también se denominan ajustes. Los valores pronosticados son las estimaciones de los puntos de la variable en el tiempo (t).
Las observaciones con valores pronosticados que sean muy diferentes del valor observado pueden ser poco comunes o influyentes. Intente identificar la causa de cualesquiera valores atípicos. Corrija cualesquiera errores de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales). A continuación, repita el análisis.
Error
Los valores de error también se denominan residuos. Los valores de error son las diferencias entre los valores observados y los pronosticados.
Interpretación
!Grafique los valores de error para determinar si su modelo es adecuado. Los valores pueden proporcionar información útil sobre el grado en que el modelo se ajusta a los datos. En general, los valores de error deberían estar aleatoriamente distribuidos alrededor de 0 sin patrones obvios ni valores poco comunes.
Período
Minitab muestra el período cuando usted genera los pronósticos. El período es la unidad de tiempo del pronóstico. Por opción predeterminada, los pronósticos comienzan al final de los datos.
Pronóstico
Los pronósticos son los valores ajustados obtenidos del modelo de series de tiempo. Minitab muestra el número de pronósticos que usted especifique. Los pronósticos comienzan al final de los datos o en el punto de origen que usted especifique.
Interpretación
Utilice los pronósticos con el fin de predecir una variable para un período de tiempo específico. Por ejemplo, la gerente de un almacén puede modelar la cantidad de productos que necesita ordenar para los próximos 3 meses con base en los pedidos de los últimos 60 meses.
Examine los ajustes y los pronósticos en la gráfica para determinar si es probable que los pronósticos sean exactos. Los ajustes deberían seguir los datos de cerca, especialmente al final de las series. Cuando se utiliza un modelo estacional, es particularmente importante verificar que los ajustes coincidan con los valores actuales al final de las series de tiempo. Si el patrón estacional o la tendencia no coinciden con los ajustes al final de los datos, es probable que los pronósticos sean menos exactos. En este caso, recolecte más datos para que el modelo se pueda adaptar a los cambios en el patrón estacional o la tendencia.
Si el modelo se ajusta a los datos al final de las series, usted puede predecir con seguridad por lo menos un ciclo estacional completo.
Inferior y superior
Los límites de predicción inferior y superior producen un intervalo de predicción para cada pronóstico. El intervalo de predicción es un rango de valores de pronósticos probables. Por ejemplo, con un intervalo de predicción de 95%, usted puede estar 95% seguro de que el intervalo de predicción contiene el pronóstico en el tiempo especificado.
Gráfica del método de Winters
La gráfica muestra las observaciones en comparación con el tiempo. La gráfica incluye los ajustes que se calcularon a partir del procedimiento de suavización, los pronósticos, la constante de suavización y las medidas de exactitud. Usted también puede elegir mostrar los valores suavizados en lugar de los ajustes.
Interpretación
- Si el modelo se ajusta a los datos, usted puede realizar Descomposición y comparar los dos modelos.
- Si el modelo no se ajusta a los datos, examine la gráfica en busca de falta de estacionalidad. Si no existe un patrón estacional, usted debería utilizar un análisis de series de tiempo diferente. Para obtener más información, vaya a ¿Cuál análisis de series de tiempo debería utilizar?.
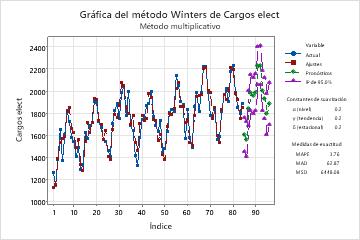
En esta gráfica, los ajustes siguen estrechamente a los datos, lo cual indica que el modelo se ajusta a los datos.
Histograma de los residuos
El histograma de los residuos muestra la distribución de los residuos para todas las observaciones. Si el modelo se ajusta a los datos, los residuos deberían ser aleatorios con una media de 0. De modo que el histograma debería exhibir simetría alrededor de 0.
Gráfica de probabilidad normal de los residuos
La gráfica normal de los residuos muestra los residuos comparados con los valores esperados cuando la distribución es normal.
Interpretación
Utilice la gráfica normal de los residuos para determinar si éstos están normalmente distribuidos. Sin embargo, este análisis no requiere residuos normalmente distribuidos.
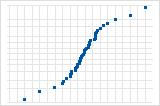
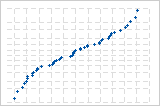
La curva S implica una distribución con colas largas.
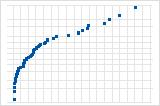
La curva S invertida implica una distribución con colas cortas.
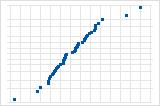
La curva hacia abajo implica una distribución asimétrica hacia la derecha.
Algunos puntos alejados de la línea implican una distribución con valores atípicos.
Residuos vs. ajustes
La gráfica de los residuos vs. los ajustes muestra los residuos en el eje Y y los valores ajustados en el eje X.
Interpretación
Utilice la gráfica de los residuos vs. los ajustes para determinar si los residuos no poseen sesgo y tienen una varianza constante. Lo ideal sería que los puntos estuvieran ubicados de manera aleatoria a ambos lados de 0, sin patrones reconocibles en los puntos.
| Patrón | Qué puede indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Varianza no constante |
| Curvilíneo | Un término de orden superior faltante |
| Un punto que está alejado de cero | Un valor atípico |
Si observa varianza no constante o patrones en los residuos, es posible que sus pronósticos no sean exactos.
Residuos vs. orden
La gráfica de los residuos vs. el orden muestra los residuos en el orden en que se recolectaron los datos.
Interpretación
Utilice la gráfica de los residuos vs. el orden para determinar con qué exactitud los ajustes se comparan con los valores ajustados durante el período de observación. Los patrones en los puntos pueden indicar que el modelo no se ajusta a los datos. Lo ideal sería que los residuos de la gráfica se ubicaran de manera aleatoria alrededor de la línea central.
| Patrón | Qué puede indicar el patrón |
|---|---|
| Una tendencia constante a largo plazo | El modelo no se ajusta a los datos |
| Una tendencia a corto plazo | Un desvío o cambio en el patrón |
| Un punto que está alejado del resto de los puntos | Un valor atípico |
| Un desvío repentino en los puntos | Un cambio en el patrón subyacente de los datos |
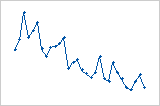
Los residuos disminuyen sistemáticamente a medida que el orden de las observaciones aumenta de izquierda a derecha.
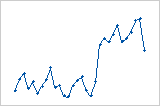
Un cambio repentino en los valores de los residuos ocurre de bajo (izquierda) a alto (derecha).
Residuos versus variables
La gráfica de los residuos vs. las variables muestra los residuos vs. otra variable.
Interpretación
Utilice la gráfica para determinar si la variable afecta la respuesta de una manera sistemática. Si hay patrones presentes en los residuos, se asocian las otras variables con la respuesta. Usted puede utilizar esta información como la base para otros estudios.
