En este tema
Lineal
Fórmula
El modelo de tendencia lineal:
Yt = β0 + β1t + et
Notación
| Término | Description |
|---|---|
| β0 | la constante |
| β1 | el cambio de promedio de un período al siguiente |
| t | el valor de la unidad de tiempo |
| et | el término de error |
Crecimiento exponencial
Fórmula
El modelo de tendencia de crecimiento exponencial representa el crecimiento o decadencia exponencial. Por ejemplo, una cuenta de ahorros pudiera mostrar crecimiento exponencial.
Yt = β0 * β1t * et
Notación
| Término | Description |
|---|---|
| β0 | la constante |
| β1 | el coeficiente |
| t | el valor de la unidad de tiempo |
| et | el término de error |
Cuadrático
Fórmula
El modelo de tendencia cuadrático, el cual puede representar una curvatura simple en los datos, es:
Yt = β0 + β1t + β2t2 + et
Notación
| Término | Description |
|---|---|
| β0 | la constante |
| β1 y β2 | los coeficientes |
| t | el valor de la unidad de tiempo |
| et | el término de error |
Curva S
Fórmula
Los datos tienen forma de S, lo cual indica que la dirección del cambio varía en el tiempo.
Yt = 10a / (β0 + β1β2t)
Notación
| Término | Description |
|---|---|
| β0 | la constante |
| β1 y β2 | los coeficientes |
| t | el valor de la unidad de tiempo |
Ponderaciones
Si usted proporciona los coeficientes del ajuste de un análisis de tendencia anterior, Minitab realiza un análisis de tendencia ponderado. Si la ponderación de un coeficiente particular es α, Minitab calcula el coeficiente nuevo por:
Fórmula
αp1 + (1 – α)p2
Notación
| Término | Description |
|---|---|
| p1 | el coeficiente estimado a partir de los datos actuales |
| p2 | coeficiente anterior |
Pronósticos
Minitab utiliza la ecuación de tendencia para calcular el pronóstico para los valores de tiempo específicos. Los datos antes del origen del pronóstico se utilizan para ajustar la tendencia.
MAPE
El error porcentual absoluto medio (EPAM) mide la exactitud de los valores ajustados de las series de tiempo. EPAM expresa la exactitud como un porcentaje.
Fórmula
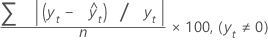
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
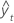 | valor ajustado |
| n | número de observaciones |
MAD
La desviación media absoluta (MAD) mide la exactitud de los valores ajustados de las series de tiempo. La MAD expresa exactitud en las mismas unidades que los datos, lo cual ayuda a conceptualizar la cantidad de error.
Fórmula
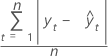
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
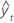 | valor ajustado |
| n | número de observaciones |
DCM
La desviación cuadrática media (DCM) siempre se calcula utilizando el mismo denominador, n, independientemente del modelo. La DCM es más sensible que DAM para medir un error de pronóstico inusualmente grande.
Fórmula
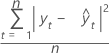
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
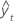 | valor ajustado |
| n | número de observaciones |
