Métodos y fórmulas para la Suavización exponencial simple

Los valores suavizados se obtienen de dos maneras: con un peso óptimo generado por Minitab o con un peso que especifiques.

Ponderación óptima de ARIMA

1. Minitab encaja con un modelo ARIMA (0,1,1) sin constante y almacena los ajustes.
2. El valor inicial suavizado para el análisis de suavizado exponencial simple es el primer ajuste no ausente del modelo ARIMA.
3. Dado que los ajustes están con lag en una sola vez, Minitab utiliza retroceso para calcular el valor inicial de ajuste (en el primer momento):
   • Valor inicial ajustado = [El primer valor suavizado – α (primer valor de datos)] / (1 – α)

Notación

Ponderación especificada

1. Minitab utiliza el promedio de las seis primeras (o N, si N < 6) observaciones para el valor inicial suavizado (en el tiempo cero). Del mismo modo, Minitab utiliza el promedio de las seis primeras (o N, s N < 6) observaciones para el valor inicial ajustado (en el tiempo uno). Ajuste (i) = Suavizado (i – 1).
2. Los valores suavizados subsiguientes se calculan a partir de la fórmula:
   • Valor suavizado en el tiempo t = α (datos en t) + (1 – α) (valor suavizado en el tiempo t – 1)

Notación

El valor ajustado en el tiempo t es el valor suavizado en el tiempo t – 1. Los pronósticos son el valor ajustado en el origen del pronóstico. Si usted pronostica 10 unidades de tiempo adelante, el valor pronosticado para cada tiempo será el valor ajustado en el origen. Los datos hasta el origen se utilizan para la suavización.

En los pronósticos ingenuos, el pronóstico para el tiempo t es el valor de los datos en el tiempo t – 1. Realice una suavización exponencial simple con una ponderación de uno para generar pronósticos ingenuos.

Fórmula

El valor de 1.25 es una constante de proporcionalidad aproximada de la desviación estándar con la desviación media absoluta. Por lo tanto, 1.25 × MAD es aproximadamente la desviación estándar.

El error porcentual absoluto medio (EPAM) mide la exactitud de los valores ajustados de las series de tiempo. EPAM expresa la exactitud como un porcentaje.

Fórmula

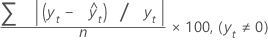
Notación

Término	Description
yt	valor real en el tiempo t
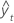	valor ajustado
n	número de observaciones

La desviación media absoluta (MAD) mide la exactitud de los valores ajustados de las series de tiempo. La MAD expresa exactitud en las mismas unidades que los datos, lo cual ayuda a conceptualizar la cantidad de error.

Fórmula

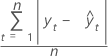
Notación

Término	Description
yt	valor real en el tiempo t
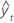	valor ajustado
n	número de observaciones

La desviación cuadrática media (DCM) siempre se calcula utilizando el mismo denominador, n, independientemente del modelo. La DCM es más sensible que DAM para medir un error de pronóstico inusualmente grande.

Fórmula

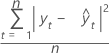
Notación

Término	Description
yt	valor real en el tiempo t
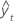	valor ajustado
n	número de observaciones