Métodos y fórmulas para la Promedio móvil

Para calcular un promedio móvil, Minitab promedia los grupos consecutivos de observaciones en una serie. Por ejemplo, supongamos que una serie comienza con los números 4, 5, 8, 9, 10 y usted utiliza la longitud de promedio móvil de 3. El tercer valor del promedio móvil es el promedio de 4, 5, 8; el cuarto valor es el promedio de 5, 8, 9; el quinto valor es el promedio de 8, 9, 10.

Por opción predeterminada, los valores de promedio móvil se colocan en el período en el cual se calculan. Por ejemplo, para una longitud de promedio móvil de 3, el primer valor de promedio móvil numérico se coloca en el período 3, el siguiente en el período 4 y así sucesivamente.

Cuando usted centra los promedios móviles, éstos se colocan en el centro del rango en lugar del final del rango. Esto se realiza para colocar los valores de promedio móvil en sus posiciones centrales en el tiempo.

Si la longitud del promedio móvil es impar

Supongamos que la longitud del promedio móvil es 3. En ese caso, Minitab coloca el primer valor de promedio móvil numérico en el período 2, el siguiente en el período 3 y así sucesivamente. En este caso, falta el valor del promedio móvil para el primer y último período ( *).

Si la longitud del promedio móvil es par

Supongamos que la longitud del promedio móvil es 4. Debido a que usted no puede colocar un valor de promedio móvil en el período 2.5, Minitab calcula el promedio de los primeros cuatro valores y les denomina MA1. Luego, Minitab calcula el promedio de los siguientes cuatro valores y los denomina MA2. El promedio de estos dos valores es el número de Minitab y lo coloca en el período 3. En este caso, los valores de promedio móvil de los dos primeros períodos y de los dos últimos períodos son valores faltantes (*).

El valor ajustado en el tiempo t es el promedio móvil no centrado en el tiempo t – 1. Los pronósticos son los valores ajustados en el origen del pronóstico. Si usted pronostica 10 unidades de tiempo adelante, el valor pronosticado para cada tiempo será el valor ajustado en el origen. Los datos hasta el origen se utilizan para calcular los promedios móviles.

Usted puede utilizar el método de promedio móvil lineal al realizar promedios móviles consecutivos. Este procedimiento se realiza con frecuencia cuando existe una tendencia en los datos. Primero, calcule y almacene el promedio móvil de las series originales. A continuación, calcule y almacene el promedio móvil de la columna almacenada previamente para obtener un segundo promedio móvil.

En pronósticos ingenuos, el pronóstico para el tiempo t es el valor de los datos en el tiempo t – 1. Al utilizar el procedimiento de promedio móvil con un promedio móvil de longitud uno se generan pronósticos ingenuos.

Fórmula

Límite superior = Pronóstico + 1.96 ×

Límite inferior = Pronóstico – 1.96 ×

Notación

El error porcentual absoluto medio (EPAM) mide la exactitud de los valores ajustados de las series de tiempo. EPAM expresa la exactitud como un porcentaje.

Fórmula

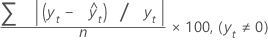
Notación

Término	Description
yt	valor real en el tiempo t
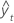	valor ajustado
n	número de observaciones

La desviación media absoluta (MAD) mide la exactitud de los valores ajustados de las series de tiempo. La MAD expresa exactitud en las mismas unidades que los datos, lo cual ayuda a conceptualizar la cantidad de error.

Fórmula

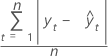
Notación

Término	Description
yt	valor real en el tiempo t
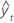	valor ajustado
n	número de observaciones

La desviación cuadrática media (DCM) siempre se calcula utilizando el mismo denominador, n, independientemente del modelo. La DCM es más sensible que DAM para medir un error de pronóstico inusualmente grande.

Fórmula

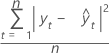
Notación

Término	Description
yt	valor real en el tiempo t
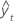	valor ajustado
n	número de observaciones