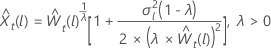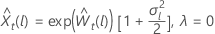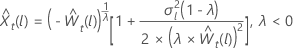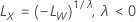Pronóstico con el mejor modelo ARIMA compara muchos modelos y selecciona un modelo final con un criterio en las especificaciones del análisis. Para obtener información sobre los resultados del modelo ARIMA final, vaya a Métodos y fórmulas para la ARIMA. Las secciones siguientes contienen detalles que son exclusivos de Pronóstico con el mejor modelo ARIMA.
Selección del modelo
La selección del modelo utiliza los siguientes pasos:
- Estimar los parámetros del modelo para cada modelo. Si un modelo incluye una constante y la estimación de los parámetros falla, intente estimar los parámetros sin el término constante.
- Calcular el criterio de información para cada modelo. El criterio predeterminado es el Criterio de información de Akaike (AICc) corregido.
- Producir resultados para el modelo con el mejor valor del criterio de información.
En las secciones siguientes se describen detalles que difieren en la selección de modelos no estacionales y estacionales.
Modelos no estacionales
- Cuando se ajustan modelos con un término constante, los modelos candidatos tienen p + q ≤ 9.
- Cuando se ajustan modelos sin un término constante, los modelos candidatos tienen p + q ≤ 10.
- Los modelos con d = 2 nunca incluyen un término constante.
- El modelo evalúa ARIMA(0, d, 0) sólo cuando d = 1.
Modelos de temporada
- Cuando se ajustan modelos con un término constante, los modelos candidatos tienen p + q + P + Q ≤ 9.
- Cuando se ajustan modelos sin un término constante, los modelos candidatos tienen p + q + P + Q ≤ 10.
- Los modelos con d + D > 1 nunca incluyen un término constante.
- La búsqueda de un modelo estacional requiere el orden de al menos uno de los parámetros estacionales para poder ser mayor que 0. La búsqueda incluye modelos no estacionales si las especificaciones para la búsqueda incluyen modelos donde todos los parámetros estacionales tienen órdenes de 0.
- Al menos 1 de p, q, P y Q es distinto de cero en cada modelo.
Criterios
- Criterio de información de Akaike (AIC)
- Criterio de información de Akaike corregido (AICc)
- Criterio de información Bayesiana (BIC)
El cálculo de los criterios de información para un modelo utiliza el valor de probabilidad logarítmica para el modelo. El cálculo del valor de logaritmos-probabilidad utiliza un algoritmo recursivo. Para obtener más información, consulte la sección 8.6 de Brockwell & Davis (1991)1.
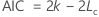
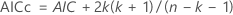

Notación
| Término | Description |
|---|---|
| k | El número de parámetros en el modelo
|
| Lc | la log-verosimilitud del modelo actual |
| n | el tamaño de la muestra de la serie temporal |
Transformación de Box-Cox
El análisis permite una transformación Box-Cox de los datos. La transformación de los datos se produce antes de la selección del modelo. Para obtener información sobre la transformación de Box-Cox para datos de series temporales, vaya a Métodos y fórmulas para Transformación de Box-Cox para Series de Tiempo.
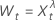 para λ > 0
para λ > 0 para λ = 0
para λ = 0 para λ < 0
para λ < 0
donde 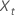 es el valor tésimo de la serie temporal original y t = 1, ..., n.
es el valor tésimo de la serie temporal original y t = 1, ..., n.
Sea 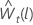 sea el valor deprevisión l ésimo a partir del origen, t, para los datos transformados. Sea
sea el valor deprevisión l ésimo a partir del origen, t, para los datos transformados. Sea  sea la varianza de pronóstico de l-paso de los datos transformados. Entonces, el valor de pronóstico lésimo de t para la serie original depende del valor de λ:
sea la varianza de pronóstico de l-paso de los datos transformados. Entonces, el valor de pronóstico lésimo de t para la serie original depende del valor de λ:
donde  es el límite en la escala original y
es el límite en la escala original y 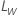 es el límite en la escala transformada.
es el límite en la escala transformada.
Modelo de caminata aleatoria
El modelo ARIMA(0, 1, 0), con o sin un término constante, es el modelo de caminata aleatoria. En Minitab Statistical Software, Pronóstico con el mejor modelo ARIMA se ajusta al modelo de caminata aleatoria. El comando requiere al menos un parámetro autorregresivo o de media móvil. Los límites de estimación y probabilidad para el modelo de caminata aleatoria tienen formas específicas. Los cálculos para la similitud logarítmica, los límites de pronóstico y los límites de probabilidad para los pronósticos dependen de si el modelo incluye un término constante.
Definiciones
| Término | Description |
|---|---|
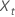 | las observaciones para una serie de tiempo con t = 1, ..., n |
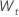 | los primeros datos diferenciados de la serie de tiempo original,  |
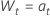
o
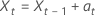
donde 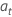 se distribuyen de forma independiente e idéntica y siguen la distribución normal con media 0 y varianza σ2, t = 2, ..., n.
se distribuyen de forma independiente e idéntica y siguen la distribución normal con media 0 y varianza σ2, t = 2, ..., n.
Las ecuaciones que representan el modelo con una constante son similares:

o
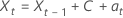

Modelo sin término constante
La log-verosimilitud tiene la siguiente forma:
log-verosimilitud
donde
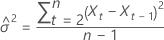

El límite de probabilidad de 100 × (1 – α) para el valor de pronóstico 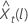 , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
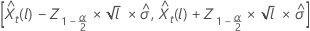
donde  representa el percentil 100 × (1 – α/2)ésimo de la distribución normal estándar.
representa el percentil 100 × (1 – α/2)ésimo de la distribución normal estándar.
Modelo con un término constante
Para un modelo con una constante, los cálculos para la log-verosimilitud requieren la estimación de la constante, C. Primero, diferenciar los datos de la serie original 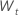 para t = 2, ..., n. La constante es la media muestral de
para t = 2, ..., n. La constante es la media muestral de 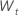 y se expresa de la siguiente forma:
y se expresa de la siguiente forma:
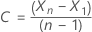
La log-verosimilitud tiene la siguiente forma:
log-verosimilitud
donde
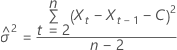
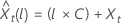
El límite de probabilidad de 100 × (1 – α) para el valor de pronóstico 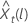 , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
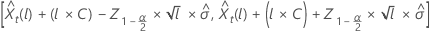
donde  representa el percentil 100 × (1 – α/2)ésimo de la distribución normal estándar.
representa el percentil 100 × (1 – α/2)ésimo de la distribución normal estándar.