Interpretación de resultados clave para Pronóstico con el mejor modelo ARIMA

Complete los siguientes pasos para interpretar el proceso de selección del modelo y los resultados para el análisis ARIMA. La salida clave incluye las estadísticas de selección de modelos, el valor p, los coeficientes, las estadísticas de chi-cuadrado de Ljung-Box y la función de autocorrelación de los residuos.

En este tema

Paso 1: Considere modelos alternativos
Paso 2: Determinar si cada término del modelo es significativo
Paso 3: Determinar si el modelo cumple con los supuestos del análisis

Paso 1: Considere modelos alternativos

La tabla Selección de modelo muestra los criterios para cada modelo de la búsqueda. La tabla muestra el orden de los términos donde p es el término autorregresivo, d es el término de diferenciación y q es el término de la media móvil. Los términos estacionales usan letras mayúsculas y los términos no estacionales usan letras minúsculas.

Utilice el AIC, el AICc y el BIC para comparar diferentes modelos. Se prefieren valores más pequeños. Sin embargo, el modelo con el menor valor para un conjunto de términos no necesariamente se ajusta bien a los datos. Utilice pruebas y gráficos para evaluar qué tan bien se ajusta el modelo a los datos. De forma predeterminada, los resultados de ARIMA son para el modelo con el mejor valor de AICc.

Seleccione Seleccionar modelo alternativo esta opción para abrir un cuadro de diálogo que incluya una tabla Selección de modelo. Compare los criterios para investigar modelos con un rendimiento similar.

Utilice la salida ARIMA para verificar que los términos del modelo son estadísticamente significativos y que el modelo cumple con los supuestos del análisis. Si ninguno de los modelos de la tabla se ajusta bien a los datos, considere modelos con diferentes órdenes de diferenciación.

También considere un modelo alternativo cuando un modelo alternativo funciona casi tan bien como el mejor modelo y tiene órdenes más bajos para los términos autorregresivos y de promedio móvil. Un modelo con menos términos es más fácil de interpretar y puede tener una mejor capacidad de previsión. Los modelos con menos términos también tienen menos probabilidades de incluir términos redundantes. Por ejemplo, los términos autorregresivos estacionales a veces son redundantes con los términos de promedio móvil estacional. Los términos redundantes a veces hacen que las estimaciones de los coeficientes sean inestables. Las siguientes son algunas de las consecuencias de los coeficientes inestables:

Los coeficientes pueden parecer insignificantes incluso cuando exista una relación significativa entre el predictor y la respuesta.
Los coeficientes de los predictores muy correlacionados variarán ampliamente de una muestra a otra.
La eliminación de cualquier término muy correlacionado del modelo afectará considerablemente los coeficientes estimados de los demás términos muy correlacionados. Los coeficientes de los términos muy correlacionados incluso pueden tener el signo equivocado.

* ADVERTENCIA * Modelos ARIMA(p, d, q) no estimables que no incluyen un término constante:
(2, 1, 2)

Selección de modelo

Modelo (d = 1)	Log-verosimilitud	AICc	AIC	BIC
p = 0, q = 2*	-197.052	400.878	400.103	404.769
p = 1, q = 2	-196.989	403.311	401.978	408.199
p = 1, q = 0	-201.327	407.029	406.654	409.765
p = 2, q = 0	-200.239	407.251	406.477	411.143
p = 1, q = 1	-200.440	407.655	406.880	411.546
p = 2, q = 1	-201.776	412.884	411.551	417.773
p = 0, q = 1	-204.584	413.542	413.167	416.278
p = 0, q = 0	-213.614	429.350	429.229	430.784

Resultados clave: AICc, BIC y AIC

El ARIMA(0, 1, 2) tiene el mejor valor de AICc. Los resultados de ARIMA que siguen son para el modelo ARIMA (0, 1, 2). Si el modelo no se ajusta lo suficientemente bien a los datos, considere otros modelos con un rendimiento similar, como el modelo ARIMA(1, 1, 2) y el modelo ARIMA (1, 1, 1). Si ninguno de los modelos se ajusta lo suficientemente bien a los datos, considere si desea utilizar un tipo diferente de modelo.

Paso 2: Determinar si cada término del modelo es significativo

Para determinar si la asociación entre la respuesta y cada término del modelo es estadísticamente significativa, compare el valor p del término con su nivel de significancia para evaluar la hipótesis nula. La hipótesis nula es que el término no es significativamente diferente de 0, lo cual indica que no existe asociación alguna entre el término y la respuesta. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0,05 indica un riesgo del 5% de concluir que el término no es significativamente diferente de 0 cuando es significativamente diferente de 0.

Valor p ≤ α: El término es estadísticamente significativo: Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que el coeficiente es estadísticamente significativo.
Valor p > α: El término no es estadísticamente significativo: Si el valor p es mayor que o igual al nivel de significancia, usted no puede concluir que el coeficiente es estadísticamente significativo. Le convendría reajustar el modelo sin el término.

Estimaciones finales de los parámetros

Tipo	Coef	SE Coef	Valor T	Valor p
AR 1	-0.504	0.114	-4.42	0.000
Constante	150.415	0.325	463.34	0.000
Media	100.000	0.216

Resultados clave: P, Coef

El término autorregresivo tiene un valor p que es menor que el nivel de significancia de 0.05. Usted puede concluir que el coeficiente del término autorregreivo es estadísticamente significativo y debería mantener el término en el modelo.

Paso 3: Determinar si el modelo cumple con los supuestos del análisis

Utilice el estadístico de chi-cuadrada de Ljung-Box y la función de autocorrelación de los residuos para determinar si el modelo cumple con los supuestos de que los residuos son independientes. Si el supuesto no se cumple, el modelo podría no ajustarse a los datos y se debería tener cuidado al interpretar los resultados.

Estadísticos de chi-cuadrada de Ljung-Box: Para determinar si los residuos son independientes, compare el valor p con el nivel de significancia. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Si el valor p es mayor que el nivel de significancia, usted puede concluir que los residuos son independientes y que el modelo cumple con el supuesto.
Función de autocorrelación de los residuos: Si no se observan correlaciones significativas, usted puede concluir que los residuos son independientes. Sin embargo, pudiera ver 1 o 2 correlaciones significativas en desfases de orden superior que no son desfases estacionales. Estas correlaciones generalmente son causadas en lugar de ello por error aleatorio y no son una señal de que el supuesto no se haya cumplido. En este caso, puede concluir que los residuos son independientes.

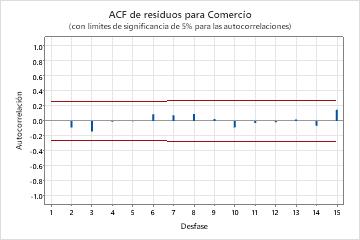
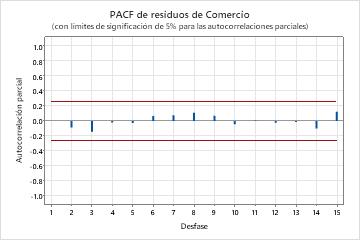
Resultados clave: Valor p, ACF de residuos
En estos resultados, los valores p de los estadísticos de chi-cuadrada de Ljung-Box son todos mayores que 0.05 y ninguna de las correlaciones para la función de autocorrelación de los residuos son significativas. Usted puede concluir que el modelo cumple con el supuesto de que los residuos son independientes.

Desfase	12	24	36	48
Chi-cuadrada	4.05	12.13	25.62	32.09
GL	10	22	34	46
Valor p	0.945	0.955	0.849	0.940