Soporte de Minitab® 

Ejemplo de Pronóstico con el mejor modelo ARIMA para un modelo estacional

Más información sobre Minitab

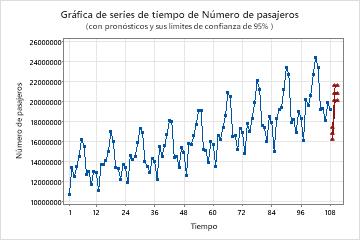
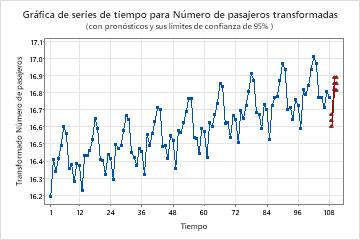
Un analista recopiló datos sobre el número de pasajeros de aerolíneas durante 108 meses. El analista quiere utilizar un modelo ARIMA para generar pronósticos para los datos. El analista examinó previamente una gráfica de series temporales de los datos y observó que la variación en el ciclo estacional aumenta con el tiempo. El analista concluyó que una transformación logarítmica natural de los datos es apropiada. Después de la transformación, el analista examinó la gráfica de series temporales de los datos transformados y la gráfica de la función de autocorrelación (ACF) de los datos transformados. Ambas gráficas sugieren que el punto de partida para el modelo es elegir 1 para el orden de diferenciación no estacional y 1 para el orden de diferenciación estacional. El analista solicita previsiones para los próximos 3 meses.

  1. Abra los datos de ejemplo PasajerosAereos.mtw.
  2. Elija Estadísticas > Series de tiempo > Pronóstico con el mejor modelo ARIMA.
  3. En Series, escriba Número de pasajeros.
  4. En Orden de diferenciación d, seleccione 1.
  5. Seleccione Ajustar modelos estacionales con período e introduzca 12 para el período.
  6. En Orden de diferenciación estacional D, seleccione 1.
  7. En Número de pronósticos, ingrese 3.
  8. Seleccione Opciones.
  9. En Transformación de Box-Cox, seleccione λ = 0 (logaritmo natural).
  10. Seleccione Aceptar en cada cuadro de diálogo.

Interpretación de los resultados

La tabla de selección de modelos clasifica los modelos de la búsqueda en orden por AICc. El modelo ARIMA(0, 1, 1)(1, 1, 0) tiene el menor AICc. Los resultados de ARIMA que siguen son para el modelo ARIMA(0, 1, 1)(1, 1, 0).

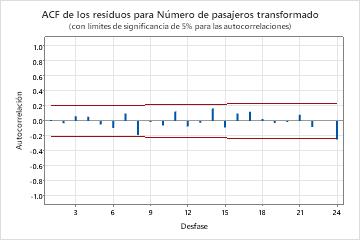
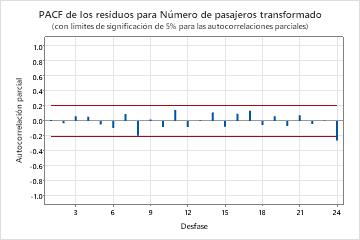
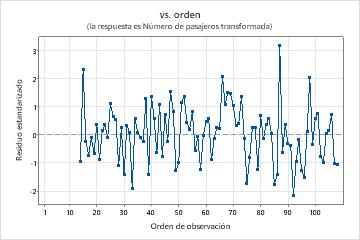
Los valores p de la tabla de parámetros muestran que los términos del modelo son significativos en el nivel de 0,05. El analista concluye que los coeficientes pertenecen al modelo. Los valores p para las estadísticas de Box-Pierce modificado (Ljung-Box) son insignificantes en el nivel de 0.05. El ACF de los residuales y el PACF de los residuales muestran un pico en el retraso 24. Debido a que un gran pico en un número de retraso alto suele ser un falso positivo y las estadísticas de la prueba son todas insignificantes, el analista concluye que el modelo cumple con la suposición de que los residuos son independientes. El analista concluye que el examen de las previsiones es razonable.

* ADVERTENCIA * Modelos ARIMA(p, d, q)(P, D, Q) no estimables que no incluyen un término constante:
(2, 1, 1)(1, 1, 1)

Método

Período estacional12
Criterio para el mejor modeloAICc mínimo
transformación de Box-Cox 
    λ especificado por el usuario0
    Series transformadas = ln(Número de pasajeros) 
Filas utilizadas108
Filas no utilizadas0

Selección de modelo

Modelo (d = 1, D = 1)Log-verosimilitudAICcAICBIC
p = 0, q = 1, P = 1, Q = 0*243.477-480.690-480.954-473.292
p = 2, q = 0, P = 0, Q = 1243.903-479.362-479.806-469.590
p = 1, q = 1, P = 1, Q = 0243.496-478.547-478.992-468.776
p = 0, q = 2, P = 1, Q = 0243.480-478.516-478.961-468.745
p = 2, q = 0, P = 1, Q = 1244.424-478.174-478.848-466.079
p = 0, q = 1, P = 0, Q = 0237.930-471.729-471.859-466.752
p = 1, q = 2, P = 0, Q = 0239.930-471.415-471.859-461.644
p = 1, q = 1, P = 0, Q = 0237.929-469.594-469.858-462.196
p = 0, q = 2, P = 0, Q = 0237.924-469.584-469.848-462.186
p = 1, q = 0, P = 0, Q = 1237.442-468.619-468.883-461.221
p = 1, q = 0, P = 1, Q = 1237.551-466.658-467.102-456.887
p = 2, q = 2, P = 0, Q = 0238.267-465.860-466.534-453.765
p = 2, q = 0, P = 0, Q = 0232.478-458.693-458.957-451.295
p = 0, q = 0, P = 0, Q = 1226.062-447.993-448.124-443.016
p = 0, q = 0, P = 1, Q = 1226.282-446.300-446.563-438.902
p = 2, q = 1, P = 0, Q = 0226.105-443.766-444.211-433.995
p = 1, q = 0, P = 0, Q = 0222.409-440.687-440.818-435.710
p = 2, q = 0, P = 1, Q = 0220.456-432.467-432.911-422.696
p = 0, q = 0, P = 1, Q = 0218.236-432.342-432.472-427.364
p = 1, q = 2, P = 1, Q = 1220.708-428.461-429.416-414.092
p = 0, q = 2, P = 0, Q = 1215.116-421.787-422.232-412.016
p = 0, q = 1, P = 0, Q = 1213.007-419.751-420.015-412.353
p = 2, q = 1, P = 0, Q = 1214.469-418.265-418.939-406.169
p = 1, q = 0, P = 1, Q = 0211.232-416.199-416.463-408.801
p = 2, q = 2, P = 0, Q = 1213.877-414.799-415.754-400.431
p = 2, q = 2, P = 1, Q = 1214.698-414.109-415.397-397.520
p = 1, q = 2, P = 0, Q = 1211.492-412.310-412.984-400.215
p = 1, q = 1, P = 0, Q = 1208.149-407.854-408.299-398.083
p = 0, q = 1, P = 1, Q = 1204.745-401.046-401.490-391.275
p = 0, q = 2, P = 1, Q = 1203.978-397.282-397.956-385.187
p = 1, q = 1, P = 1, Q = 1203.564-396.453-397.127-384.358
p = 1, q = 2, P = 1, Q = 0170.812-330.950-331.624-318.855
p = 2, q = 2, P = 1, Q = 0167.845-322.735-323.690-308.367
p = 2, q = 1, P = 1, Q = 0-202.538415.751415.076427.846
* Mejor modelo con AICc mínimo. La siguiente es la salida del mejor modelo.

Estimaciones finales de los parámetros

TipoCoefSE CoefValor TValor p
ARE  12-0.4030.103-3.920.000
PM   10.87040.051017.080.000
Diferenciación: 1 regular, 1 estacional de orden 12
Número de observaciones después de la diferenciación: 95

Resumen del modelo

GLSCMCMSDAICcAICBIC
930.03113260.00033480.0003277-480.690-480.954-473.292
CM = varianza de las series de ruido blanco

Estadístico de chi-cuadrada modificado de Box-Pierce (Ljung-Box)

Desfase12243648
Chi-cuadrada9.4726.4433.9950.66
GL10223446
Valor p0.4890.2330.4680.295
* ADVERTENCIA * Modelos ARIMA(p, d, q)(P, D, Q) no estimables que no incluyen un término constante:
(2, 1, 1)(1, 1, 1)

Series originales

Período
de tiempo
Límites de 95%
PronósticoInferiorSuperiorActual
109168226641622724217434097 
110208238762008075121587153 
111208267022007744321596450 

Series transformadas



Pronóstico
del error
estándar


Período
de tiempo
Límites de 95%
PronósticoInferiorSuperiorActual
10916.63810.018296416.602216.6739 
11016.85140.018449516.815316.8876 
11116.85160.018601416.815116.8880 
Copyright © 2024 Minitab, LLC. All rights Reserved.