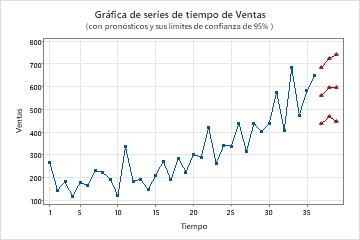
Ejemplo de Pronóstico con el mejor modelo ARIMA para un modelo no estacional

Un analista de marketing quiere utilizar un modelo ARIMA para generar pronósticos a corto plazo para las ventas de un producto de champú. El analista recopila datos de ventas de los tres años anteriores. El analista examinó previamente una gráfica de series temporales y la gráfica de la función de autocorrelación (ACF) para la serie. Ambas gráficas sugieren 1 como punto de partida para el orden de diferenciación no estacional. Los datos no exhiben un patrón estacional en una gráfica de series temporales, por lo que el analista elige comenzar con un modelo no estacional. El analista solicita previsiones para los próximos 3 meses.

Abra los datos de ejemplo VentasChampú.MTW.
Elija Estadísticas > Series de tiempo > Pronóstico con el mejor modelo ARIMA.
En Series, escriba Ventas.
En Orden de diferenciación d, seleccione 1.
Desmarque Incluir el término de constante en los modelos.
En Número de pronósticos, ingrese 3.
Seleccione Aceptar.

Interpretación de los resultados

La tabla de selección de modelos clasifica los modelos de la búsqueda en orden por AICc. El modelo ARIMA(0, 1, 2) tiene el menor AICc. Los resultados de ARIMA que siguen son para el modelo ARIMA (0, 1, 2).

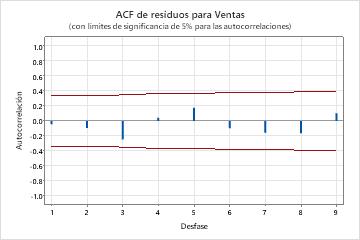
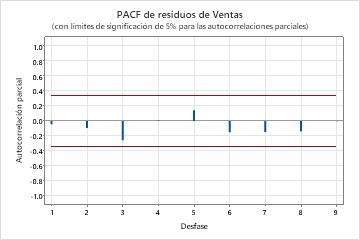
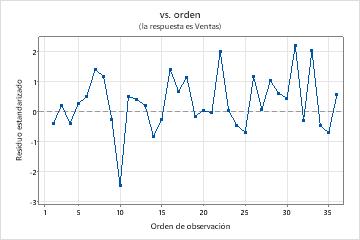
Los valores p en la tabla de parámetros muestran que los términos de la media móvil son significativos en el nivel de 0.05. El analista concluye que los coeficientes pertenecen al modelo. Los valores p para las estadísticas de Box-Pierce modificado (Ljung-Box) son insignificantes en el nivel de 0.05. El ACF de los residuos y el PACF de los residuos están todos dentro de los límites de 0.05 en sus respectivas parcelas. El analista concluye que el modelo satisface el supuesto de que los residuos son independientes. El analista concluye que el examen de las previsiones es razonable.

Criterio para el mejor modelo	AICc mínimo
Filas utilizadas	36
Filas no utilizadas	0

Modelo (d = 1)	Log-verosimilitud	AICc	AIC	BIC
p = 0, q = 2*	-197.052	400.878	400.103	404.769
p = 1, q = 2	-196.989	403.311	401.978	408.199
p = 1, q = 0	-201.327	407.029	406.654	409.765
p = 2, q = 0	-200.239	407.251	406.477	411.143
p = 1, q = 1	-200.440	407.655	406.880	411.546
p = 2, q = 1	-201.776	412.884	411.551	417.773
p = 0, q = 1	-204.584	413.542	413.167	416.278
p = 0, q = 0	-213.614	429.350	429.229	430.784

Tipo	Coef	SE Coef	Valor T	Valor p
PM 1	1.257	0.132	9.52	0.000
PM 2	-0.882	0.133	-6.62	0.000

Desfase	12	24	36	48
Chi-cuadrada	15.90	27.15	*	*
GL	10	22	*	*
Valor p	0.103	0.206	*	*

		Pronóstico del error estándar
Período de tiempo			Límites de 95%
Período de tiempo	Pronóstico		Inferior	Superior	Actual
37	563.193	63.0096	439.669	686.717
38	594.912	65.0499	467.388	722.435
39	594.912	76.0553	445.813	744.010

Ejemplo de Pronóstico con el mejor modelo ARIMA para un modelo no estacional

Interpretación de los resultados

Método

Selección de modelo

Estimaciones finales de los parámetros

Resumen del modelo

Estadístico de chi-cuadrada modificado de Box-Pierce (Ljung-Box)

Pronósticos del período de tiempo 36