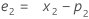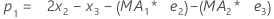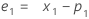En este tema
Ecuación del modelo
La suavización exponencial doble utiliza un componente de nivel y un componente de tendencia en cada período. La suavización exponencial doble utiliza dos ponderaciones (que también se conocen como parámetros de suavización) para actualizar los componentes en cada período. Las ecuaciones de la suavización exponencial doble son las siguientes:
Fórmula
Lt= αYt+ (1 – α) [Lt–1 + Tt–1]
Tt= γ [Lt – Lt–1] + (1 – γ) Tt–1
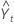 = Lt−1
+ Tt−1
= Lt−1
+ Tt−1
Si la primera observación se enumera con el número uno, entonces las estimaciones de nivel y tendencia en el tiempo cero deben inicializarse para poder continuar. El método de inicialización solía determinar cómo se obtienen los valores suavizados de dos maneras: con las ponderaciones óptimas o con las ponderaciones especificadas.
Notación
| Término | Description |
|---|---|
| Lt | el nivel en el tiempo t |
| α | la ponderación del nivel |
| Tt | la tendencia en el tiempo t |
| γ | la ponderación para la tendencia |
| Yt | ll valor de los datos en el tiempo t |
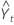 | el valor pronosticado para el tiempo t |
Ponderaciones
Ponderaciones óptimas de ARIMA
- Minitab ajusta con un modelo ARIMA (0,2,2) los datos para minimizar la suma de errores cuadrados.
- Los componentes de tendencia y nivel son entonces inicializados por retroproyección.
Ponderaciones especificadas
- Minitab ajusta un modelo de regresión lineal a los datos de las series de tiempo (variable Y) en función del tiempo (variable X).
- La constante de esta regresión es la estimación inicial del componente de nivel, el coeficiente de la pendiente es la estimación inicial del componente de tendencia.
Cuando se especifican ponderaciones que corresponden a un modelo ARIMA (0, 2, 2) con raíz igual, el método de Holt se especializa en el método de Brown 1.
Método para calcular los valores iniciales para nivel y tendencia
puede almacenar estimaciones para nivel y tendencia. Minitab utiliza uno de los métodos siguientes para calcular los valores de la primera fila de estas columnas, en función de las opciones que se especifiquen en el cuadro de diálogo.
Si elige la opción ARIMA óptimo en Suavización exponencial doble, Minitab utiliza el siguiente método para calcular los primeros valores de nivel y tendencia. Puede realizar estos pasos de forma manual.
- Elija para calcular valores de ponderación óptima utilizando ARIMA. Complete el cuadro de diálogo como se indica enseguida:
- En Autorregresivo, ingrese 0.
- En Diferencia, ingrese 2.
- En Promedio móvil, ingrese 2.
- Elimine la selección de Incluir término de constante en modelo.
- Haga clic en Almacenamiento y seleccione Residuos. Haga clic en Aceptar en cada cuadro de diálogo.
- Minitab utiliza los valores MA del resultado de ARIMA
para calcular las ponderaciones óptimas de la siguiente manera:
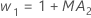
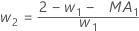
- A continuación, Minitab vuelve a calcular la observación inicial, utilizando datos de observaciones posteriores:
donde:
Término Description pi el valor pronosticado de la iésima observación suavizada xi el valor de la iésima observación en las series de tiempo ei el valor del iésimo residuo, almacenado a partir del resultado de ARIMA obtenido previamente -
- Minitab calcula el valor inicial para el nivel (L1):

- Minitab calcula el valor inicial para la tendencia (T1):
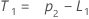
- Cree una columna de índices de tiempo iguales a la longitud de su columna de datos de series de tiempo. Una columna de enteros de 1 a n es suficiente.
- Elija .
- En Respuestas, ingrese una columna de datos de series de tiempo. En Predictores continuos, ingrese la columna de índices de tiempo.
- Haga clic en Almacenamiento y seleccione Coeficientes. Haga clic en Aceptar en cada cuadro de diálogo.
- El valor inicial para el nivel es:
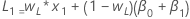
- El valor inicial para la tendencia es:
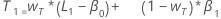 donde:
donde:Término Description L1 valor inicial para el nivel x1 el valor de la primera observación en las series de tiempo T1 valor inicial para la tendencia wL el valor de ponderación para el nivel wT el valor de ponderación para la tendencia β0 el coeficiente del término constante en el modelo de regresión β1 el coeficiente para el término del predictor en el modelo de regresión
Pronósticos
La suavización exponencial doble utiliza los componentes de nivel y de tendencia para generar pronósticos. El pronóstico para m períodos adelante desde un punto en el tiempo t es el siguiente:
Fórmula
Lt + mTt
Los datos hasta el tiempo de origen del pronóstico se utilizan para la suavización.
Notación
| Término | Description |
|---|---|
| Lt | el nivel en el tiempo t |
| Tt | la tendencia en el tiempo t |
Límites de predicción
Fórmula
- Límite superior = Pronóstico + 1.96 × dt × MAD
- Límite inferior = Pronóstico – 1.96 × dt × MAD
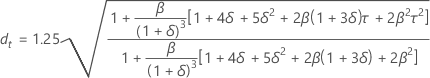
Notación
| Término | Description |
|---|---|
| β | máx{α, γ) |
| δ | 1 – β |
| α | constante de suavización de nivel |
| γ | constante de suavización de tendencia |
| τ |  |
| b0(T) | 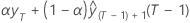 |
| b1(T) | 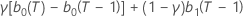 |
MAPE
El error porcentual absoluto medio (EPAM) mide la exactitud de los valores ajustados de las series de tiempo. EPAM expresa la exactitud como un porcentaje.
Fórmula
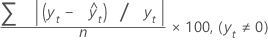
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
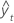 | valor ajustado |
| n | número de observaciones |
MAD
La desviación media absoluta (MAD) mide la exactitud de los valores ajustados de las series de tiempo. La MAD expresa exactitud en las mismas unidades que los datos, lo cual ayuda a conceptualizar la cantidad de error.
Fórmula
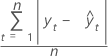
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
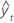 | valor ajustado |
| n | número de observaciones |
DCM
La desviación cuadrática media (DCM) siempre se calcula utilizando el mismo denominador, n, independientemente del modelo. La DCM es más sensible que DAM para medir un error de pronóstico inusualmente grande.
Fórmula
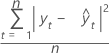
Notación
| Término | Description |
|---|---|
| yt | valor real en el tiempo t |
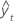 | valor ajustado |
| n | número de observaciones |