En este tema
Transformación de Box-Cox
La transformación de Box-Cox viene dada por la siguiente fórmula:
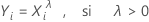
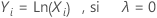

donde Xi es un valor de datos original y λ es el parámetro para la transformación. Cuando el análisis busca el valor óptimo de λ, el análisis redondea el valor óptimo de λ a 0,5 o al entero más cercano para realizar la transformación.
Valores comunes de λ
| λ | Transformación |
|---|---|
| 2 | 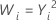 |
| 0.5 |  |
| 0 |  |
| -1 |  |
Búsqueda de la λ óptima
- Definir el criterio para que el valor óptimo sea un coeficiente mínimo de variación.
- Divide la serie en subserie H .
- Utilice el método de Brent para encontrar el valor de λ que minimice el coeficiente de variación.
Las siguientes secciones definen la subserie y el coeficiente de variación.
Subserie
Divide la serie en subserie por período estacional. Si el período estacional no se divide uniformemente en la serie, omita las observaciones restantes del comienzo de la serie. Si las especificaciones para el análisis no incluyen un período estacional, establezca el período estacional = 2.
Por ejemplo, supongamos una serie temporal original con 10 observaciones y un período estacional de 4: {5, 6, 3, 2, 9, 8, 1, 7, 10, 4}. El número de subserie es 10 módulo 4 = 2. Debido a que 4 no se divide uniformemente en 10, use solo las últimas 8 observaciones para formar la subserie. Las subserie son {3, 2, 9, 8} y {1, 7, 10, 4}.
Valores faltantes
Si una subserie contiene 1 o más valores faltantes, omita la subserie de los cálculos en la búsqueda del valor óptimo de λ. La búsqueda requiere al menos 2 subseries sin valores faltantes.
Coeficiente de variación
Utilice las siguientes definiciones para calcular el coeficiente de variación:| Término | Description |
|---|---|
| X1, X2, ... XN | las observaciones en la serie temporal original |
| P | el período estacional de la serie temporal original |
| Xh, i | la iésima observación en la subserie h, donde i=1, ..., P y h=1, ..., H |
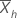 | la media muestral de la subserie hésima |
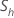 | la desviación típica de la muestra de la subserie hésima |
Las siguientes ecuaciones definen las estadísticas de cada subserie:
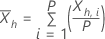
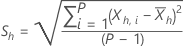
Para un λ dado y para h=1, ..., H utiliza la siguiente definición:
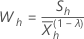
Calcule el promedio de la muestra y la desviación estándar de la muestra para las estadísticas W :

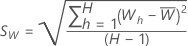

Utilice el método de Brent para encontrar el valor de λ que minimiza el CV en el intervalo a partir de las especificaciones para el análisis. El análisis redondea el valor óptimo de λ a 0,5 o al entero más cercano para realizar la transformación.
