Un analista recopiló datos sobre el número de pasajeros de aerolíneas durante 108 meses. El analista quiere utilizar un modelo ARIMA para generar pronósticos para los datos. En una gráfica de series temporales, el analista ve que la diferencia entre los picos estacionales altos y bajos crece con el tiempo. Este patrón indica que la varianza no es estacionaria. El analista realiza una transformación de Box-Cox para hacer que la varianza sea estacionaria antes de que el analista se ajuste al modelo ARIMA.
- Abra los datos de ejemplo PasajerosAereos.MWX.
- Elija .
- En Series, escriba Número de pasajeros.
- En Período estacional, ingrese 12.
- Seleccione λ óptimo esta opción para que Minitab Statistical Software busque una transformación para usar.
- En Columna de marca de tiempo para la escala de tiempo, escriba Fecha.
- En Almacenar las series transformadas en, ingrese Transformado. Haga clic en Aceptar.
Interpretar los resultados
La tabla Método muestra la configuración para el análisis y el valor de λ para la transformación.
En estos resultados, el período estacional es 12 y el análisis busca un valor λ entre el rango predeterminado de -1 y 2. El valor óptimo para λ es aproximadamente -0.14. El análisis redondea el valor a 0 y utiliza la transformación logarítmica natural.
Método
| Período estacional | 12 |
|---|---|
| Seleccionar λ óptimo en intervalo | [-1, 2] |
| λ óptimo | -0.144439 |
| λ óptimo redondeado | 0 |
| Series transformadas = ln(Número de pasajeros) |
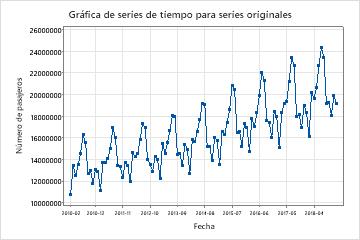
Compare la serie temporal de la serie original con la gráfica de la serie temporal de la serie transformada para comprobar que la transformación hace que la varianza sea estacionaria.
En estos resultados, la gráfica de la serie temporal de la serie original muestra la varianza no estacionaria. En estos datos, la diferencia entre los puntos altos y bajos en un ciclo estacional aumenta a medida que pasa el tiempo. Este patrón muestra que la varianza aumenta a medida que pasa el tiempo.
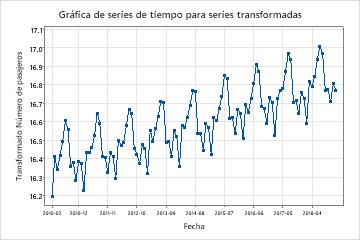
Examine la gráfica de series temporales de la serie transformada para comprobar que la transformación hace que la varianza sea estacionaria.
En estos resultados, la gráfica de series temporales de la serie transformada muestra una diferencia aproximadamente pareja entre los puntos altos y bajos en los ciclos estacionales. Este patrón muestra que la transformación hace que la varianza sea estacionaria.
Examine también la gráfica de series temporales de los datos transformados para evaluar otras características importantes de la serie transformada. Por ejemplo, los supuestos para un modelo ARIMA incluyen que la serie tiene una media estacionaria además de una varianza estacionaria. Si una gráfica de serie temporal de la serie transformada muestra que la serie transformada no tiene una media estacionaria, intente Prueba de Dickey-Fuller aumentada ver si la diferenciación de los datos hace que la media de la serie sea estacionaria.
En estos resultados, la serie transformada muestra una tendencia al alza. Este patrón muestra que la media de la serie no es estacionaria. Utilice la Prueba de Dickey-Fuller aumentada columna en la columna almacenada de datos transformados para determinar si la diferenciación hace que la serie sea estacionaria.