La función de autocorrelación es una medida de la correlación entre las observaciones de una serie de tiempo separadas por k unidades de tiempo (yt e yt–k).
Interpretación
Utilice la función de autocorrelación y las funciones de autocorrelación parcial conjuntamente para identificar modelos ARIMA. Examine los picos en cada desfase para determinar si son significativos. Un pico significativo se extenderá más allá de los límites de significancia, lo cual indica que la correlación para ese desfase no es igual a cero.
Nota
Los datos deben ser estacionarios antes de que usted interprete la gráfica de autocorrelación. Una serie de tiempo estacionaria tiene una media, una varianza y una función de autocorrelación que son esencialmente constantes a través del tiempo. Para obtener más información, vaya a Consideraciones acerca de los datos para la función de autocorrelación.
| Patrón | Lo que indica el patrón | Ejemplo |
|---|---|---|
| Pico grande en el desfase 1 que disminuye después de unos pocos desfases. | Un término autorregresivo en los datos. Utilice la función de correlación parcial para determinar el orden del término autorregresivo. | 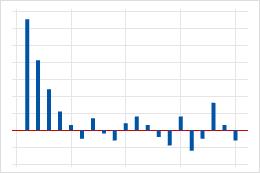 |
| Pico grande en el desfase 1 seguido por una onda decreciente que alterna entre correlaciones positivas y negativas. | Un término autorregresivo de orden superior en los datos. Utilice la función de autocorrelación parcial para determinar el orden del término autorregresivo. | 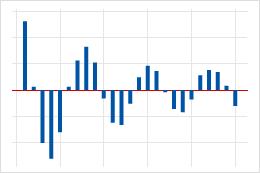 |
| Correlaciones significativas en el primer o segundo desfase, seguidas por correlaciones que no son significativas. | Un término de promedio móvil en los datos. El número de correlaciones significativas indica el orden del término de promedio móvil. | 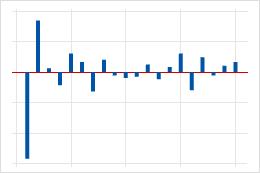 |
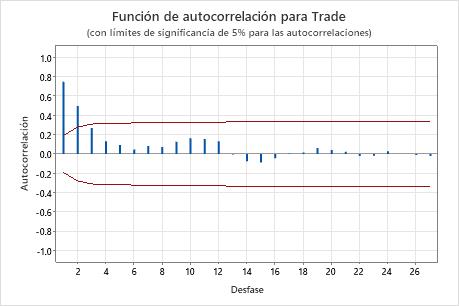
En esta gráfica, hay una correlación significativa en el desfase 1 que disminuye después de unos pocos desfases. Esta patrón indica un término autorregresivo. Usted debe utilizar la función de autocorrelación parcial para determinar el orden del término autorregresivo.
