Modelos de regresión
| Término | Description |
|---|---|
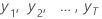 | los valores de las series temporales observadas en el tiempo = 1, ..., T |
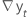 | la diferencia de dos observaciones consecutivas en el tiempo t, 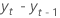 , donde t = 2, ..., T , donde t = 2, ..., T |
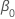 | el término constante en un modelo de regresión |
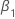 | el coeficiente de una tendencia de tiempo lineal en un modelo de regresión |
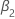 | el coeficiente de una tendencia de tiempo cuadrática en un modelo de regresión |
 | el orden de retraso del proceso autorregresivo |
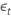 | el término de error independiente en serie en el momento t para t = 2, ..., T |
- Un modelo con sólo un coeficiente constante

- Un modelo con un coeficiente constante y un coeficiente lineal
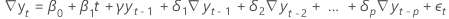
- Un modelo con un coeficiente constante, un coeficiente lineal y un coeficiente cuadrático

- Un modelo sin coeficientes de regresión
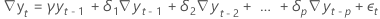
Hipótesis
Cada prueba de Augmented Dickey-Fuller utiliza las siguientes hipótesis:
Hipótesis nula, H0: 
Hipótesis alternativa, H1: 
La hipótesis nula dice que una raíz unitaria está en la muestra de la serie temporal, lo que significa que la media de los datos no es estacionaria. Rechazar la hipótesis nula indica que la media de los datos es estacionaria o estacionaria de tendencia, dependiendo del modelo para la prueba.
Estadístico de prueba

donde
| Término | Description |
|---|---|
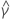 | la estimación del coeficiente mínimo cuadrado de la 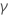 coeficiente coeficiente |
 | el error estándar de la estimación de mínimos cuadrados de la  coeficiente del modelo de regresión coeficiente del modelo de regresión |
Valores p aproximados de MacKinnon
Bajo la hipótesis nula, la distribución asintótica de la estadística de prueba no sigue una distribución estándar. Fuller (1976)1 proporciona una tabla con percentiles comunes de la distribución asintótica. MacKinnon (19942, 20103) aplica aproximaciones de la superficie de respuesta a los datos simulados para proporcionar un valor p aproximado para cualquier valor de la estadística de prueba ADF.
Si las especificaciones para el análisis utilizan 0.01, 0.05 o 0.1 como nivel de significancia, entonces la evaluación de la hipótesis nula compara la estadística de prueba con el valor crítico para ese nivel de significación. Si la estadística de prueba es menor o igual que el valor crítico, rechace la hipótesis nula.
Si las especificaciones para el análisis dan un nivel de significancia diferente, entonces la evaluación de la hipótesis nula compara el valor p aproximado con el nivel de significación. Si el valor p es menor que el nivel de significancia, rechace la hipótesis nula.
Valores críticos para los niveles de significancia 0,01, 0,05 y 0,1
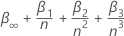
donde n es el número de observaciones que el análisis utiliza para ajustarse al modelo de regresión. Los valores de 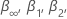 y
y  provienen de mesas en MacKinnon (2010). Si la estadística de prueba es menor o igual que el valor crítico, rechace la hipótesis nula.
provienen de mesas en MacKinnon (2010). Si la estadística de prueba es menor o igual que el valor crítico, rechace la hipótesis nula.
Valores p aproximados
El cálculo del valor p aproximado proviene de Mackinnon (1994). Compare el valor p con el nivel de significancia para tomar una decisión. Si el valor p es menor o igual que el nivel de significancia, rechace la hipótesis nula.
Determinación del orden de retraso

La selección del orden de retraso depende del criterio en las especificaciones del análisis. Si las especificaciones para el análisis no incluyen un criterio, entonces el modelo de regresión para la prueba es el orden máximo de p.
En los cálculos para determinar el orden de retraso, el número de observaciones depende del orden de retraso máximo tal que m = n – p – 1.
| Término | Description |
|---|---|
| n | el número total de observaciones |
| p | el orden de retraso máximo de los términos diferenciados que se encuentran en el modelo |
El cálculo de cada criterio es el siguiente:
Criterio de información de Akaike (AIC)
El análisis evalúa un modelo de regresión para cada orden de retraso en las especificaciones del análisis. El orden de retraso para la prueba es el modelo de regresión con el valor mínimo del AIC.
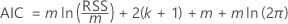
donde
| Término | Description |
|---|---|
| m | el número de observaciones que depende del orden de retraso máximo |
| k | el número de coeficientes del modelo, incluida la constante si el modelo de regresión tiene una constante distinta de cero |
| RSS | la suma residual de cuadrados del modelo de regresión |
Criterio de información Bayesiana (BIC)
El análisis evalúa un modelo de regresión para cada orden de retraso en las especificaciones del análisis. El orden de retraso para la prueba es el modelo de regresión con el valor mínimo del BIC.
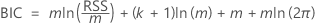
donde
| Término | Description |
|---|---|
| m | el número de observaciones que depende del orden de retraso máximo |
| k | el número de coeficientes del modelo, incluida la constante si el modelo de regresión tiene una constante distinta de cero |
| RSS | la suma residual de cuadrados del modelo de regresión |
estadístico t
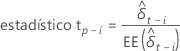
donde i = 1, ..., p
| Término | Description |
|---|---|
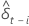 | la estimación de mínimos cuadrados de la  coeficiente en el modelo de regresión coeficiente en el modelo de regresión |
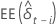 | el error estándar de la estimación de mínimos cuadrados de la  coeficiente en el modelo de regresión coeficiente en el modelo de regresión |
