En este tema
Tabla de métodos
La tabla Método muestra la configuración del análisis y el orden de retraso seleccionado.
En estos resultados, el orden máximo de retraso que evalúa el análisis es 9. El análisis utiliza el modelo con el orden de retraso más alto de 4 para calcular los resultados de la prueba.
Método
| Orden de desfase máximo para los términos del modelo de regresión | 9 |
|---|---|
| Criterio para seleccionar el orden de desfase | AIC mínimo |
| Términos adicionales | Constante |
| Orden de desfase seleccionado | 4 |
| Filas utilizadas | 36 |
Tabla de Prueba de Dickey-Fuller Aumentada
La tabla Prueba de Dickey-Fuller Aumentada proporciona las hipótesis, una estadística de prueba, un valor p y una recomendación sobre si considerar la diferenciación para hacer que la serie sea estacionaria.
La estadística de la prueba proporciona una forma de evaluar la hipótesis nula. Las estadísticas de prueba que son menores o iguales al valor crítico proporcionan evidencia contra la hipótesis nula.
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades inferiores proporcionan mayor evidencia en contra de la hipótesis nula.
Para determinar si se deben diferenciar los datos, compare la estadística de prueba con el valor crítico o el valor p con su nivel de significación. Debido a que el valor p contiene más aproximación, la recomendación del análisis utiliza el valor crítico para evaluar la hipótesis nula cuando el nivel de significancia es 0,01, 0,05 o 0,10. Por lo general, la conclusión es la misma para el valor crítico y el valor p. La hipótesis nula es que los datos no son estacionarios, lo que implica que la diferenciación es un paso razonable para tratar de hacer que los datos sean estacionarios.
- Valor P ≤ nivel de significación
- Estadística de prueba ≤ valor crítico
- Si el valor p es menor o igual que el nivel de significancia o si la estadística de prueba es menor o igual que el valor crítico, la decisión es rechazar la hipótesis nula. Debido a que los datos proporcionan evidencia de que los datos son estacionarios, la recomendación del análisis es proceder sin diferencias.
- Valor P > nivel de significación
- Estadística de prueba > valor crítico
- Si el valor p es mayor que el nivel de significancia o si la estadística de prueba es mayor que el valor crítico, la decisión es no rechazar la hipótesis nula. Debido a que los datos no proporcionan evidencia de que los datos sean estacionarios, la recomendación del análisis es determinar si la diferenciación hace que la media de los datos sea estacionaria.
En estos resultados, la estadística de prueba de 2.29045 es mayor que el valor crítico de aproximadamente -2.96053. Debido a que los resultados no rechazan la hipótesis nula de que los datos no son estacionarios, la recomendación de la prueba es considerar la diferenciación para hacer que los datos sean estacionarios.
Prueba de Dickey-Fuller aumentada
| Hipótesis nula: | Los datos son no estacionarios |
|---|---|
| Hipótesis alterna: | Los datos son estacionarios |
| Estadística de prueba | Valor p | Recomendación |
|---|---|---|
| 2.29045 | 0.999 | Estadístico de prueba > valor crítico de -2.96053. |
| Nivel de significancia = 0.05 | ||
| No rechace la hipótesis nula. | ||
| Considere diferenciar para hacer que los datos sean estacionarios. |
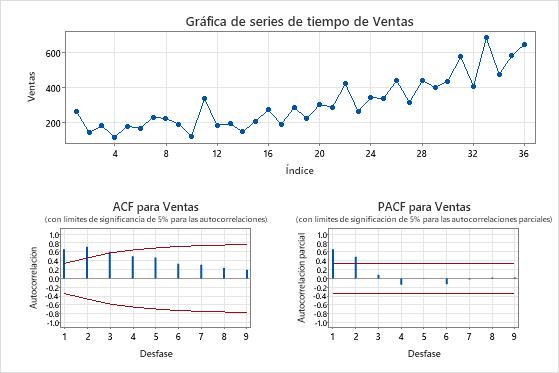
Diagramas de la serie original
- Gráfica de series de tiempo
- Utilice la gráfica de series temporales de la serie original para examinar las características de los datos originales. Una tendencia es un ejemplo de un patrón que indica una media no estacionaria. Use la diferenciación para tratar de hacer que la media sea estacionaria.
- Gráfica ACF
- Utilice la función de autocorrelación (ACF) de los datos originales para buscar un patrón que indique que la media de los datos no es estacionaria. Un patrón común son los picos grandes a través de los retrasos que se extinguen muy lentamente.
- Gráfica PACF
- Por lo general, se utiliza la función de autocorrelación parcial (PACF) de datos estacionarios para buscar patrones que indiquen la presencia de términos autorregresivos en un modelo ARIMA. Si los datos originales no son estacionarios, utilice la gráfica PACF de la serie diferenciada para buscar términos candidatos para el modelo ARIMA.
En estos resultados, los datos muestran una tendencia creciente en la gráfica de series temporales. El primer retraso en la gráfica ACF muestra un gran pico que excede el límite de significación del 5%, luego disminuye muy lentamente. Estos patrones indican que la media de los datos no es estacionaria.
Debido a que las ventas no tienen relación con un predictor que explique una tendencia determinista y el analista quiere usar un modelo ARIMA para pronosticar las ventas, diferenciar los datos es una forma razonable de tratar de hacer que la media de la serie sea estacionaria.
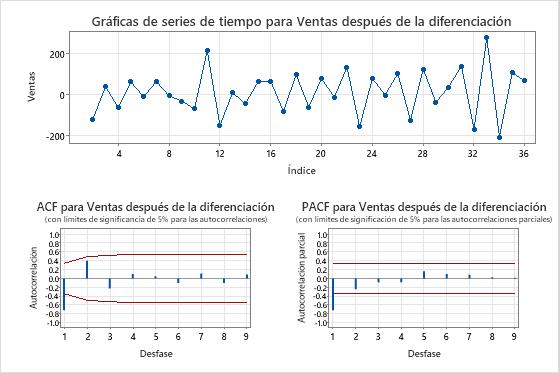
Diagramas de las series diferenciadas
- Diagrama de series temporales después de la diferenciación
- Utilice la gráfica de series temporales de los datos diferenciados para comprobar que la diferenciación hace que la media de los datos sea estacionaria. La gráfica de series temporales muestra las diferencias entre observaciones consecutivas. Los datos con una media estacionaria siguen una trayectoria horizontal en la gráfica de series temporales.
- Diagrama ACF y gráfico PACF después de la diferenciación
- Utilice el ACF de los datos diferenciados para verificar que la diferenciación hace que la media de los datos sea estacionaria. Los gráficos con picos que disminuyen rápidamente son característicos de los datos estacionarios.
En estos resultados, la gráfica de series temporales muestra que la media y la varianza de los datos diferenciados son aproximadamente constantes. Los datos parecen estar estacionarios.
En la gráfica ACF de los datos diferenciados, el único pico que es significativamente diferente de 0 es en el retraso 1. Este patrón también sugiere que los datos son estacionarios.