Un analista de marketing quiere utilizar un modelo ARIMA para generar pronósticos a corto plazo para las ventas de un producto de champú. El analista recopila datos de ventas de los tres años anteriores. En un gráfico de series temporales, el analista ve que los datos tienden al alza. Este patrón indica que la media de los datos no es estacionaria. El analista realiza una prueba aumentada de Dickey-Fuller para determinar el orden de diferenciación no estacional a incluir en el modelo ARIMA. Para obtener más información sobre los modelos ARIMA, vaya a Revisión general de ARIMA.
- Abra los datos de ejemplo VentasChampú.MWX.
- Elija .
- En Series, escriba Ventas.
- Seleccione Aceptar.
Interpretación de los resultados
En estos resultados, la estadística de prueba de 2.29045 es mayor que el valor crítico de -2.96053. Debido a que los resultados no rechazan la hipótesis nula de que los datos no son estacionarios, la recomendación de la prueba es considerar la diferenciación de primer orden para hacer que los datos sean estacionarios.
Método
| Orden de desfase máximo para los términos del modelo de regresión | 9 |
|---|---|
| Criterio para seleccionar el orden de desfase | AIC mínimo |
| Términos adicionales | Constante |
| Orden de desfase seleccionado | 4 |
| Filas utilizadas | 36 |
Prueba de Dickey-Fuller aumentada
| Hipótesis nula: | Los datos son no estacionarios |
|---|---|
| Hipótesis alterna: | Los datos son estacionarios |
| Estadística de prueba | Valor p | Recomendación |
|---|---|---|
| 2.29045 | 0.999 | Estadístico de prueba > valor crítico de -2.96053. |
| Nivel de significancia = 0.05 | ||
| No rechace la hipótesis nula. | ||
| Considere diferenciar para hacer que los datos sean estacionarios. |
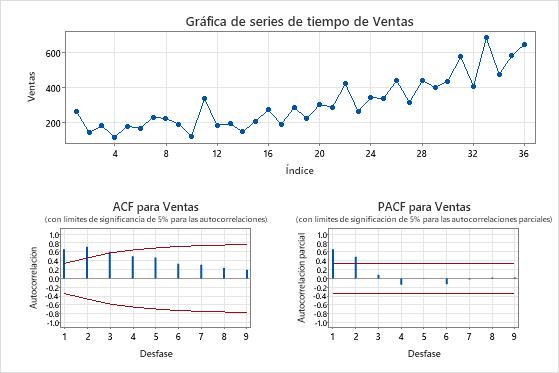
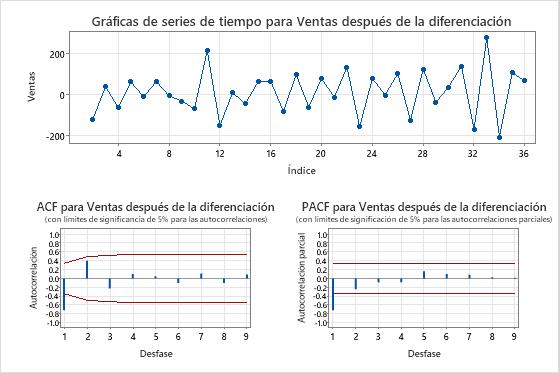
Las diagramas de series temporales muestran el resultado de la diferenciación. En estos resultados, la gráfica de series temporales de los datos originales muestra una tendencia clara. La gráfica de series temporales de los datos diferenciados muestra las diferencias entre valores consecutivos. Los datos diferenciados parecen estacionarios porque los puntos siguen un camino horizontal sin patrones obvios en la variación.
Las gráficas de ACF también muestran el efecto de la diferenciación. En estos resultados, la gráfica ACF de los datos originales muestra picos disminuidos lentamente a través de los retrasos. Este patrón indica que los datos no son estacionarios. En la gráfica ACF de los datos diferenciados, el único pico que es significativamente diferente de 0 es en el retraso 1.
En estos resultados, las gráficas de series temporales y las gráficas ACF confirman los resultados de la prueba. Por lo tanto, un enfoque razonable es diferenciar los datos y luego ajustar un modelo autorregresivo y de media móvil para hacer pronósticos.