En este tema
Coeficientes
Los coeficientes se estiman utilizando un algoritmo iterativo que calcula las estimaciones de mínimos cuadrados. En cada iteración, se calculan los pronósticos retrospectivos y la SSE. Para obtener más detalles, consulte Box y Jenkins1.
El algoritmo de ARIMA se basa en la rutina de ajuste en el paquete TSERIES escrito por el profesor William Q. Meeker, Jr., de Iowa State University2. Agradecemos al profesor Meeker su ayuda en la adaptación de esta rutina para Minitab.
Pronósticos retrospectivos
Los pronósticos retrospectivos se calculan utilizando el modelo especificado y las estimaciones de los parámetros de la iteración actual. Para mayor información, véase Cryer3.
SSE
Fórmula
Notación
| Término | Description |
|---|---|
| n | número total de observaciones |
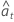 | residuos que utilizan estimaciones de parámetros de dicha iteración, incluyendo pronósticos retrospectivos |
SC para residuos
Fórmula
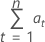
Notación
| Término | Description |
|---|---|
| n | número total de observaciones |
| at | los residuos que utilizan las estimaciones finales de los parámetros, sin tomar en cuenta los pronósticos retrospectivos |
GL para residuos
Fórmula
Para un modelo con un término de constante:
(n – d) – p – q – 1
Para un modelo sin un término de constante:
(n – d) – p – q
Notación
| Término | Description |
|---|---|
| n | número total de observaciones |
| d | número de diferencias |
| p | número de parámetros autorregresivos incluidos en el modelo |
| q | número de parámetros de promedio móvil incluidos en el modelo |
CM para residuos
Fórmula
SC / GL
Estadístico de chi-cuadrado
Fórmula
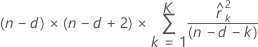
Notación
| Término | Description |
|---|---|
| n | número total de observaciones |
| d | número de diferencias |
| K | 12, 24, 36, 48 |
| k | desfase |
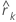 | autocorrelación de los residuos para el desfase késimo |
GL para estadístico de chi-cuadrado
Fórmula
Para un modelo con un término de constante:
K – p – q – 1
Para un modelo sin un término de constante:
K – p – q
Notación
| Término | Description |
|---|---|
| K | 12, 24, 36, 48 |
| p | número de parámetros autorregresivos incluidos en el modelo |
| q | número de parámetros de promedio móvil incluidos en el modelo |
Valor p para estadístico chi-cuadrado
Fórmula
P(X < χ2)
Notación
| Término | Description |
|---|---|
| X | distribuido como χ2(DF) |
Pronósticos
Fórmula
Los pronósticos se calculan de manera recursiva, según el modelo y las estimaciones de los parámetros. Por ejemplo, si un modelo ARIMA se ajusta con 1 término autorregresivo (AR(1)) y un término de diferenciación estacional con un período estacional de 12, este modelo está ajustado:
Yt – Yt–12 = γ + Φ(Yt–1 – Yt–12–1)
para estimar 
, el primer pronóstico, donde k es el origen, busque:
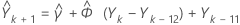
Luego, busque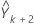 
, de la misma manera, y así sucesivamente.
Para calcular el intervalo de predicción de 95% para la previsión, primero debe calcular las ponderaciones.
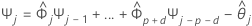
donde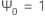 
, 
para j < 0, y 
para j > q.
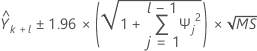
Notación
| Término | Description |
|---|---|
| Yt | valor real en el tiempo t |
| Φ | término autorregresivo |
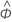 | término autorregresivo estimado |
| γ | término constante |
| d | número de diferencias |
| p | número de parámetros autorregresivos |
| q | número de parámetros de promedio móvil |
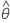 | término de promedio móvil estimado |
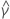 | término constante estimado |
| MC | cuadrado medio del error |
