En este tema
Paso 1: Determinar si cada término en el modelo es estadísticamente significativo
- Valor p ≤ α: El término es estadísticamente significativo
- Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que el coeficiente es estadísticamente significativo.
- Valor p > α: El término no es estadísticamente significativo
- Si el valor p es mayor que o igual al nivel de significancia, usted no puede concluir que el coeficiente es estadísticamente significativo. Le convendría reajustar el modelo sin el término.
Estimaciones finales de los parámetros
| Tipo | Coef | SE Coef | Valor T | Valor p |
|---|---|---|---|---|
| AR 1 | -0.504 | 0.114 | -4.42 | 0.000 |
| Constante | 150.415 | 0.325 | 463.34 | 0.000 |
| Media | 100.000 | 0.216 |
Resultados clave: P, Coef.
El término autorregresivo tiene un valor p que es menor que el nivel de significancia de 0.05. Usted puede concluir que el coeficiente del término autorregreivo es estadísticamente significativo y debería mantener el término en el modelo.
Paso 2: Determinar hasta qué punto el modelo se ajusta a los datos
Utilice el cuadrado medio del error (CM) para determinar qué tan bien se ajusta el modelo a los datos. Valores más pequeños indican un modelo de ajuste más adecuado.
Sumas de los cuadrados de los residuos
| GL | SC | MC |
|---|---|---|
| 58 | 366.733 | 6.32299 |
Resultados clave: CM
El cuadrado medio del error es 6.323 para este modelo. El valor no ofrece mucha información por sí solo, pero lo puede utilizar para comparar los ajustes de diferentes modelos de ARIMA.
Paso 3: Determinar si el modelo cumple con los supuestos del análisis
- Estadísticos de chi-cuadrada de Ljung-Box
- Para determinar si los residuos son independientes, compare el valor p con el nivel de significancia. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Si el valor p es mayor que el nivel de significancia, usted puede concluir que los residuos son independientes y que el modelo cumple con el supuesto.
- Función de autocorrelación de los residuos
- Si no se observan correlaciones significativas, usted puede concluir que los residuos son independientes. Sin embargo, pudiera ver 1 o 2 correlaciones significativas en desfases de orden superior que no son desfases estacionales. Estas correlaciones generalmente son causadas en lugar de ello por error aleatorio y no son una señal de que el supuesto no se haya cumplido. En este caso, puede concluir que los residuos son independientes.
Estadístico de chi-cuadrada modificado de Box-Pierce (Ljung-Box)
| Desfase | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| Chi-cuadrada | 4.05 | 12.13 | 25.62 | 32.09 |
| GL | 10 | 22 | 34 | 46 |
| Valor p | 0.945 | 0.955 | 0.849 | 0.940 |
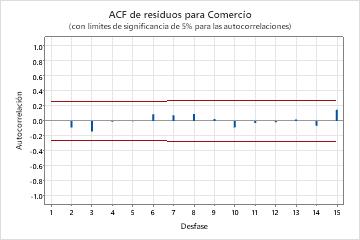
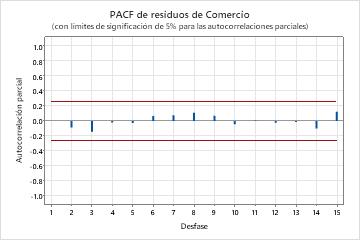
Resultados clave: Valor p, ACF de residuos
En estos resultados, los valores p de los estadísticos de chi-cuadrada de Ljung-Box son todos mayores que 0.05 y ninguna de las correlaciones para la función de autocorrelación de los residuos son significativas. Usted puede concluir que el modelo cumple con el supuesto de que los residuos son independientes.
