En este tema
Gráfica de series de tiempo
La gráfica de series de tiempo muestra los datos en orden cronológico. Cuando usted genera pronósticos, Minitab muestra los pronósticos y sus niveles de confianza de 95% en la gráfica.
Interpretación
- Determine si hay variaciones diferentes presentes en los datos. Si las hubiera, entonces debe transformar los datos para que la varianza sea constante.
- Determine si los datos están centrados alrededor de una media constante. Si la media no es constante, es posible que deba diferenciar los datos para convertirla en constante.
ACF de residuos
La gráfica muestra la función de autocorrelación de los residuos. La función de autocorrelación es una medida de la correlación entre las observaciones de una serie de tiempo separadas por k unidades de tiempo (yt e yt–k).
Interpretación
Utilice la función de autocorrelación de los residuos para determinar si el modelo satisface los supuestos de que los residuos son independientes. Si no se satisface el supuesto, es posible que el modelo no se ajuste a los datos y usted debería ser precavido cuando interprete los resultados. Si no hay correlaciones significativas presentes, entonces usted puede concluir que los residuos son independientes. Sin embargo, pueden observarse 1 o 2 correlaciones significativas en desfases de mayor orden no estacionales. Estos desfases generalmente se deben a un error aleatorio y no representan una señal de que no se satisface el supuesto. De modo que, en este caso, usted también puede concluir que los residuos son independientes.
PACF de residuos
La función de autocorrelación parcial es una medida de la correlación entre las observaciones de una serie de tiempo que se encuentran separadas por k unidades de tiempo (yt y yt–k), después de ajustarse para la presencia de los demás términos de desfase más corto (yt–1, yt–2, ..., yt–k–1).
Interpretación
Utilice la función de autocorrelación parcial de los residuos para determinar si el modelo satisface los supuestos de que los residuos son independientes. Si no se satisface el supuesto, es posible que el modelo no se ajuste a los datos y usted debería ser precavido cuando interprete los resultados. Si no hay correlaciones significativas presentes, entonces usted puede concluir que los residuos son independientes.
Histograma de los residuos
El histograma de los residuos muestra la distribución de los residuos para todas las observaciones. Si el modelo se ajusta a los datos, los residuos deberían ser aleatorios con una media de 0. De modo que el histograma debería exhibir simetría alrededor de 0.
Gráfica de probabilidad normal de los residuos
La gráfica normal de los residuos muestra los residuos comparados con los valores esperados cuando la distribución es normal.
Interpretación
Utilice la gráfica normal de los residuos para determinar si éstos están normalmente distribuidos. Sin embargo, este análisis no requiere residuos normalmente distribuidos.
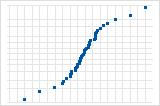
La curva S implica una distribución con colas largas.
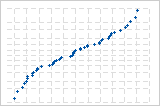
La curva S invertida implica una distribución con colas cortas.
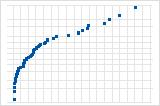
La curva hacia abajo implica una distribución asimétrica hacia la derecha.
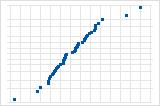
Algunos puntos alejados de la línea implican una distribución con valores atípicos.
Residuos vs. ajustes
La gráfica de los residuos vs. los ajustes muestra los residuos en el eje Y y los valores ajustados en el eje X.
Interpretación
Utilice la gráfica de los residuos vs. los ajustes para determinar si los residuos no poseen sesgo y tienen una varianza constante. Lo ideal sería que los puntos estuvieran ubicados de manera aleatoria a ambos lados de 0, sin patrones reconocibles en los puntos.
| Patrón | Qué puede indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Varianza no constante |
| Curvilíneo | Un término de orden superior faltante |
| Un punto que está alejado de cero | Un valor atípico |
Si observa varianza no constante o patrones en los residuos, es posible que sus pronósticos no sean exactos.
Residuos vs. orden
La gráfica de los residuos vs. el orden muestra los residuos en el orden en que se recolectaron los datos.
Interpretación
Utilice la gráfica de los residuos vs. el orden para determinar con qué exactitud los ajustes se comparan con los valores ajustados durante el período de observación. Los patrones en los puntos pueden indicar que el modelo no se ajusta a los datos. Lo ideal sería que los residuos de la gráfica se ubicaran de manera aleatoria alrededor de la línea central.
| Patrón | Qué puede indicar el patrón |
|---|---|
| Una tendencia constante a largo plazo | El modelo no se ajusta a los datos |
| Una tendencia a corto plazo | Un desvío o cambio en el patrón |
| Un punto que está alejado del resto de los puntos | Un valor atípico |
| Un desvío repentino en los puntos | Un cambio en el patrón subyacente de los datos |
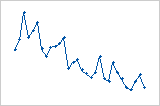
Los residuos disminuyen sistemáticamente a medida que el orden de las observaciones aumenta de izquierda a derecha.
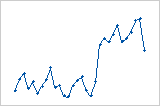
Un cambio repentino en los valores de los residuos ocurre de bajo (izquierda) a alto (derecha).
Residuos versus variables
La gráfica de los residuos vs. las variables muestra los residuos vs. otra variable.
Interpretación
Utilice la gráfica para determinar si la variable afecta la respuesta de una manera sistemática. Si hay patrones presentes en los residuos, se asocian las otras variables con la respuesta. Usted puede utilizar esta información como la base para otros estudios.
