Un grupo de ingenieros desea evaluar la fiabilidad de una carcasa de compresor rediseñada para motores de reacción. Para evaluar el diseño, los ingenieros utilizan una máquina para lanzar un proyectil individual en cada carcasa de compresor. Después del impacto del proyectil, los ingenieros inspeccionan el compresor cada doce horas en busca de fallas.
Los ingenieros realizan la regresión con datos de vida útil para evaluar la relación entre el diseño de la carcasa, el peso del proyectil y el tiempo hasta la falla. También desean estimar los tiempos hasta la falla en los que pueden esperar que fallen entre el 1% y el 5% de los motores. Los ingenieros utilizan una distribución de Weibull para modelar los datos.
- Abra los datos de muestra, MtrReaciónFiab.MWX.
- Elija .
- Seleccione Las respuestas son datos no cens./censurados arbitrariamente.
- En Variables/Variables iniciales, ingrese Inicio.
- En Variables finales, ingrese Fin.
- En Modelo, ingrese Diseño y Ponderación.
- En Factores (opcional), ingrese Diseño.
- Haga clic en Estimar. En Ingresar nuevos valores predictores, ingrese Nuevo diseñoNueva ponderación.
- En Estimar percentiles para porcentajes, ingrese 1 5 y luego haga clic en Aceptar.
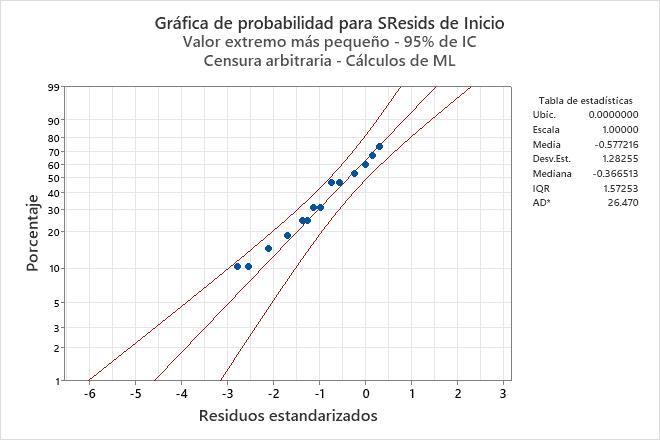
- Haga clic en Gráficas. Seleccione Gráfica de probabilidad para residuos estandarizados.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
En la tabla de regresión, los valores p para diseño y peso son significativos en un nivel α de 0.05. Por lo tanto, los ingenieros concluyen que tanto el diseño de la caja como el peso del proyectil tienen un efecto estadísticamente significativo en los tiempos de falla. Los coeficientes de los predictores se pueden utilizar para definir una ecuación que describa la relación entre el diseño de la caja, el peso del proyectil y el tiempo de falla para los motores.
La tabla de percentiles muestra los percentiles 1 y 5 para cada combinación de diseño de caja y peso de proyectil. El tiempo que transcurre antes que 1% o 5% de los motores falle es más largo para el diseño de la nueva caja que para el diseño de la caja estándar, en todos los pesos del proyectil. Por ejemplo, después de ser sometido a un proyectil de 10 libras, se puede esperar que 1% de los motores con un diseño de caja estándar falle después de aproximadamente 101.663 horas. Con el diseño de la nueva caja, se puede esperar que 1% de los motores falle después de aproximadamente 205.882 horas.
La gráfica de probabilidad de los residuos estandarizados muestra que los puntos siguen una línea aproximadamente recta. Por lo tanto, los ingenieros pueden presuponer que el modelo es apropiado.
Censura
| Información de censura | Conteo |
|---|---|
| Valor censurado por la derecha | 25 |
| Valor censurado del intervalo | 23 |
Tabla de regresión
| Error estándar | IC normal de 95.0% | |||||
|---|---|---|---|---|---|---|
| Predictor | Coef | Z | P | Inferior | Superior | |
| Intersección | 6.68731 | 0.193766 | 34.51 | 0.000 | 6.30754 | 7.06709 |
| Diseño | ||||||
| Estándar | -0.705643 | 0.0725597 | -9.72 | 0.000 | -0.847857 | -0.563428 |
| Ponderación | -0.0565899 | 0.0212396 | -2.66 | 0.008 | -0.0982187 | -0.0149611 |
| Forma | 5.79286 | 1.07980 | 4.02001 | 8.34755 | ||
Bondad de ajuste (ajustado) de Anderson-Darling
Tabla de percentiles
| Error estándar | IC normal de 95.0% | |||||
|---|---|---|---|---|---|---|
| Porcentaje | Diseño | Ponderación | Percentil | Inferior | Superior | |
| 1 | Estándar | 5.0 | 134.911 | 17.6574 | 104.385 | 174.363 |
| 1 | Estándar | 7.5 | 117.113 | 16.0279 | 89.5591 | 153.144 |
| 1 | Estándar | 10.0 | 101.663 | 16.3830 | 74.1295 | 139.423 |
| 1 | Nueva | 5.0 | 273.214 | 36.8022 | 209.819 | 355.763 |
| 1 | Nueva | 7.5 | 237.171 | 32.6878 | 181.028 | 310.726 |
| 1 | Nueva | 10.0 | 205.882 | 32.8675 | 150.568 | 281.518 |
| 5 | Estándar | 5.0 | 178.749 | 16.9676 | 148.404 | 215.300 |
| 5 | Estándar | 7.5 | 155.168 | 14.1107 | 129.836 | 185.443 |
| 5 | Estándar | 10.0 | 134.698 | 15.4568 | 107.568 | 168.670 |
| 5 | Nueva | 5.0 | 361.994 | 36.0778 | 297.761 | 440.084 |
| 5 | Nueva | 7.5 | 314.239 | 28.8741 | 262.450 | 376.247 |
| 5 | Nueva | 10.0 | 272.783 | 30.6102 | 218.928 | 339.887 |