En este tema
- Estimación puntual de un percentil para un porcentaje determinado
- Error estándar de un percentil para un porcentaje dado
- Intervalo de confianza fiducial de un percentil para un porcentaje determinado
- Intervalo de confianza fiducial de la probabilidad de fallo o de supervivencia a un valor de tensión dado
- Referencias
Estimación puntual de un percentil para un porcentaje determinado
El punto percentil p, xp, es el nivel de estrés necesario para una respuesta p.
Para encontrar la estimación de xp, use la siguiente fórmula:
donde 
y 
son las estimaciones de máxima verosimilitud de 
y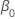 
.
Las distribuciones de ubicación logarítmica para el análisis Probit son las distribuciones lognormal, loglogistic y Weibull. En el caso de las distribuciones de ubicación logarítmica, las fórmulas anteriores estiman el percentil en la escala logarítmica. Para estimar el percentil en la escala de los datos con estas distribuciones, utilice la siguiente fórmula.
Error estándar de un percentil para un porcentaje dado
El cálculo del error estándar de un percentil utiliza el método delta. El error estándar del percentil estimado tiene la siguiente fórmula.
donde la varianza de 
, se expresa de la siguiente forma:
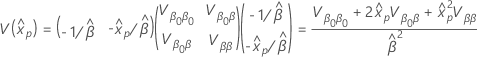
y la matriz de varianza-covarianza de 
y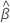 
, se expresa de la siguiente forma:
Las distribuciones de ubicación logarítmica para el análisis Probit son las distribuciones lognormal, loglogistic y Weibull. En el caso de las distribuciones de ubicación logarítmica, las fórmulas anteriores estiman la varianza de 
. Definiciones de la varianza y de la matriz de varianza-covarianza en términos de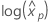 
seguir.
Intervalo de confianza fiducial de un percentil para un porcentaje determinado
El bilateral, 100(1 - 
) para 
es 
con las siguientes ecuaciones.
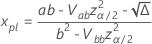
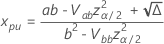
donde
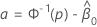
Las distribuciones de ubicación logarítmica para el análisis Probit son las distribuciones lognormal, loglogistic y Weibull. En el caso de las distribuciones de ubicación logarítmica, las fórmulas anteriores estiman el intervalo en la escala de registro. Para estimar el intervalo en la escala de los datos, exponencialice los límites de confianza en las fórmulas anteriores.
Intervalo de confianza fiducial de la probabilidad de fallo o de supervivencia a un valor de tensión dado
El bilateral, 100(1 - 
) para la probabilidad de fallo, 
, es 
. Para la probabilidad de supervivencia, 
, el intervalo es 
. Las siguientes fórmulas dan los cálculos.
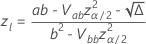
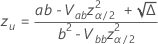
donde
y 
es la función de distribución acumulativa de la distribución para el análisis.
Las distribuciones de ubicación logarítmica para el análisis Probit son las distribuciones lognormal, loglogistic y Weibull. En el caso de las distribuciones de ubicación de registros, sustitúyase la siguiente definición.
Referencias
La derivación de los intervalos de confianza fiduciales utiliza el teorema de Fieller. El teorema de Fieller se encuentra en la siguiente referencia.
Finney, D. J. (1971). Probit analysis, (Third edition), London: Cambridge University Press.
Para más información sobre el modelo probit y la estimación de percentiles, consulte la siguiente referencia.
Cox, D. R. and Snell, E. J. (1989). The analysis of binary data (Second edition), London: Chapman & Hall.
