En este tema
Gráfica de probabilidad
- Puntos de la gráfica, que son los percentiles estimados para las probabilidades correspondientes de un conjunto de datos ordenados.
- Línea ajustada, que es el percentil esperado de la distribución con base en estimaciones del parámetro de máxima verosimilitud.
- Intervalos de confianza, que son los intervalos de confianza de los percentiles.
Debido a que los puntos de la gráfica no dependen de ninguna distribución, serían los mismos (antes de ser transformados) para cualquier gráfica de probabilidad que se elabore. Sin embargo, la línea ajustada difiere dependiendo de la distribución paramétrica que se haya elegido. De esta manera, puede utilizar la gráfica de probabilidad para evaluar si una distribución en particular se ajusta a sus datos. En general, mientras más cerca se encuentren los puntos de la línea ajustada, mejor será el ajuste.
Puntos de la gráfica
- Método de rango de medianas (predeterminado)
- Método de Kaplan-Meier modificado
- Método de Herd-Johnson
- Método de Kaplan-Meier
Si los datos contienen tiempos de falla empatados (tiempos de falla idénticos), se grafican todos los puntos (opción predeterminada), el promedio (mediana) o el máximo de los puntos emparados. Si el empate involucra fallas y suspensiones, se condiera que las fallas ocurren antes que las suspensiones.
Cada uno de estos métodos genera estimaciones no paramétricas de F(t), la función de distribución acumulada de la variable aleatoria T, que es tiempo para fallar.
Para una muestra de n observaciones, sean x(1), x(2),...,x(n) los estadísticos de orden o los datos ordenados del menor al mayor. Entonces i es el rango de la I ésima observación ordenada x(I). La fórmula de cada método es la siguiente:
Rango de medianas (método de Benard)
Fórmula para datos no censurados
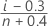
Fórmula para datos censurados

Kaplan-Meier modificado
Fórmula para datos no censurados
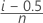
Fórmula para datos censurados
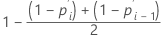
Estimación de Herd-Johnson
Fórmula para datos no censurados

Fórmula para datos censurados
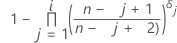
Estimación de Kaplan-Meier de límite de producto
Nota
Si la observación más grande no tiene censura, el método de Kaplan-Meier da como resultado p = 1 para la observación no censurada más grande. En este caso, la estimación de Kaplan-Meier para la observación más grande da como resultado un número que no se puede utilizar en la gráfica. Este problema se corrige volviendo a calcular el p más grande como 90% de la distancia entre el p anterior y 1.
Nota
Para datos censurados arbitrariamente, Minitab estima las probabilidades acumuladas utilizando el método de Turnbull1.
Fórmula para datos no censurados

Fórmula para datos censurados
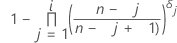
Notación
| Término | Description |
|---|---|
| i | rango de los punto de datos, con rangos consecutivos asignados a los empates |
| n | número de observaciones en los datos |
| δj | 0 si la j ésima observación está censurada o 1 si la j ésima observación no tiene censura |
| ARi |
 |
| AR0 | es igual a 0 |
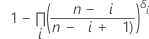
| p'i |
 |
Línea ajustada
- Minitab transforma el eje X a una escala logarítmica cuando usted utiliza la distribución de Weibull, Weinbull de 3 parámetros, exponencial, lognormal o loglogística.
- Minitab transforma el eje Y a una escala porcentual por opción predeterminada. Si usted cambia el tipo de la escala Y a probabilidad, Minitab transforma el eje Y a una escala de probabilidad.
| Distribución | coordenada X | coordenada Y |
|---|---|---|
| Valor extremo más pequeño | tiempo de falla | ln(–ln(1 – p)) |
| Weibull | ln(tiempo de falla) | ln(–ln(1 – p)) |
| Weibull de 3 parámetros | ln(tiempo de falla) – valor umbral) | ln(–ln(1 – p)) |
| Exponencial | ln(tiempo de falla) | ln(–ln(1 – p)) |
| Exponencial de 2 parámetros | ln(tiempo de falla) – valor umbral) | ln(–ln(1 – p)) |
| Normal | tiempo de falla | Φ –1 (p) |
| Lognormal | ln(tiempo de falla) | Φ –1 (p) |
| Lognormal de 3 parámetros | ln(tiempo de falla) – valor umbral) | Φ –1 (p) |
| Logística | tiempo de falla |
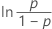 |
| Loglogística | ln(tiempo de falla) |
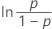 |
| Loglogística de 3 parámetros | ln(tiempo de falla) – valor umbral) |
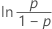 |
Notación
| Término | Description |
|---|---|
| Φ –1 | cdf inversa de la distribución normal estándar |
| ln (x) | logaritmo natural de x |
