En este tema
Gráfica de probabilidad
Utilice la gráfica de probabilidad para evaluar en qué grado la distribución que usted seleccionó se ajusta a sus datos. Si los puntos siguen de cerca la línea ajustada, entonces puede presuponer que la distribución se ajusta a los datos razonablemente bien.
- Los puntos de la gráfica son los percentiles estimados con base en un método no paramétrico que no depende de ninguna distribución. Cuando usted detiene el cursor en un punto de datos, Minitab muestra el tiempo de falla observado y la probabilidad acumulada estimada.
- La línea ajustada (línea central) se basa en la distribución ajustada. Cuando usted detiene el cursor en la línea ajustada, Minitab muestra una tabla de percentiles de varios porcentajes.
- La línea izquierda conecta los bordes inferiores en los intervalos de confianza para cada percentil. La línea derecha conecta los bordes superiores en los intervalos de confianza para cada percentil.
Ejemplo de salida
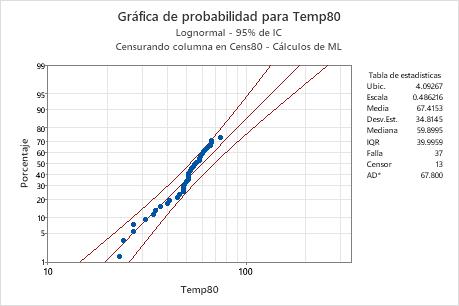
Interpretación
Para la muestra Temp80 de los datos sobre bobinas de motor, los puntos parecen seguir la línea ajustada. Por lo tanto, usted puede presuponer que la distribución lognormal es una opción apropiada para los datos. La línea ajustada se basa en una distribución lognormal con ubicación = 4.09267 y escala = 0.486216.
Gráfica de supervivencia
La gráfica de supervivencia ilustra la probabilidad de que el elemento sobreviva hasta un tiempo particular. Por lo tanto, la gráfica de supervivencia muestra la fiabilidad del producto en el tiempo.
- La línea central es la fiabilidad estimada en el tiempo.
- La línea derecha conecta los bordes superiores de la fiabilidad en cada punto de tiempo. La línea izquierda conecta los bordes inferiores de la fiabilidad en cada punto de tiempo.
Cuando usted detiene el cursor en la curva de supervivencia, Minitab muestra una tabla de tiempos de falla y probabilidades de supervivencia.
Utilice esta gráfica solo cuando la distribución se ajuste adecuadamente a los datos. Si la distribución no se ajusta adecuadamente a los datos, estos estimados serán inexactos. Utilice la gráfica de ID de distribución, gráfica de probabilidad y medidas de bondad de ajuste para determinar si la distribución se ajusta adecuadamente a los datos.
Ejemplo de salida
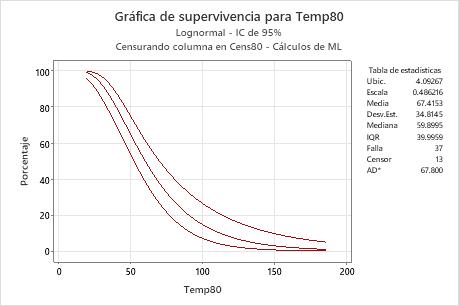
Interpretación
Para los datos sobre bobinas de motor, la probabilidad de que las bobinas de motor sobrevivan a una temperatura de 80º C durante por lo menos 50 horas es de aproximadamente 60%. La función de supervivencia se basa en la distribución lognormal con ubicación = 4.09267 y escala = 0.486216.
Gráfica de falla acumulada
Para describir la fiabilidad del producto en términos del momento en que este falla, la gráfica de falla acumulada muestra el porcentaje acumulado de elementos que fallan a un tiempo particular, t. La función de falla acumulada representa 1 − función de supervivencia.
- La línea central es el porcentaje de falla acumulado estimado en el tiempo.
- La línea derecha conecta los bordes inferiores para el porcentaje de falla acumulado en cada punto de tiempo. La línea izquierda conecta los bordes superiores del porcentaje de falla acumulado en cada punto de tiempo.
Cuando usted detiene el cursor sobre la curva, Minitab muestra la probabilidad de falla acumulada y el tiempo de falla.
Utilice esta gráfica solo cuando la distribución se ajuste adecuadamente a los datos. Si la distribución no se ajusta adecuadamente a los datos, estos estimados serán inexactos. Utilice la gráfica de ID de distribución, gráfica de probabilidad y medidas de bondad de ajuste para determinar si la distribución se ajusta adecuadamente a los datos.
Ejemplo de salida
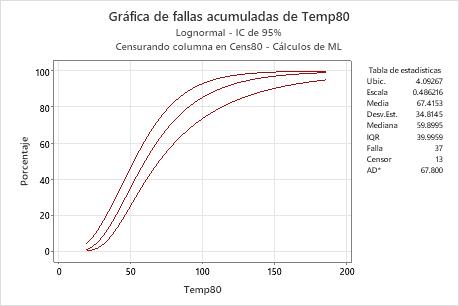
Interpretación
Para los datos sobre bobinas de motor, la probabilidad de que las bobinas de motor fallen a las 70 horas a una temperatura de 80º C es de aproximadamente 60%. La función de falla acumulada se basa en la distribución lognormal con ubicación = 4.09267 y escala = 0.486216.
Gráfica de riesgo
- Decreciente: Los elementos tienen menor probabilidad de fallar con el paso del tiempo. Un riesgo decreciente ocurre comúnmente en el período inicial de la vida de un producto.
- Constante: Los elementos fallan a una tasa constante. Un riesgo constante ocurre comúnmente durante la "vida útil" de un producto cuando las fallas ocurren aleatoriamente.
- Creciente: Los elementos tienen mayor probabilidad de fallar con el paso del tiempo. Un riesgo creciente ocurre comúnmente en las etapas finales de la vida de un producto, como el desgaste.
La forma de función de riesgo se determina con base en los datos y la distribución elegida. Cuando usted detiene el cursor en la curva de riesgo, Minitab muestra una tabla de tiempos de falla y tasas de riesgo.
Utilice esta gráfica solo cuando la distribución se ajuste adecuadamente a los datos. Si la distribución no se ajusta adecuadamente a los datos, estos estimados serán inexactos. Utilice la gráfica de ID de distribución, gráfica de probabilidad y medidas de bondad de ajuste para determinar si la distribución se ajusta adecuadamente a los datos.
Ejemplo de salida
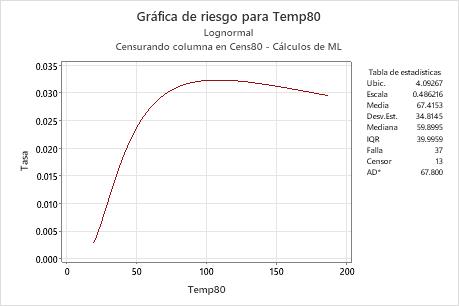
Interpretación
Para la variable Temp80 de los datos sobre bobinas de motor, la función de riesgo se basa en la distribución lognormal con ubicación = 4.09267 y escala = 0.486216. A una temperatura de 80° C, la tasa de riesgo aumenta hasta aproximadamente 100 horas, luego disminuye lentamente.
Gráficas de múltiples modos de falla
Para los datos sobre múltiples fallas, Minitab muestra gráficas para cada modo de falla.
- Utilice la gráfica de probabilidad para determinar en qué grado se ajusta a los datos la distribución elegida. Si los puntos siguen de cerca la línea ajustada, entonces utilice esa distribución para modelar los datos.
- Utilice la gráfica de supervivencia para evaluar la probabilidad de que el elemento sobreviva hasta un tiempo particular. De esta manera, la gráfica de supervivencia muestra la confiabilidad del producto en el tiempo.
- Utilice la función de riesgo para proveer la probabilidad de falla como una función de la duración de una unidad (la tasa de falla instantánea en un tiempo particular, t). La gráfica de riesgo muestra la tendencia en la tasa de fallas en el tiempo.
Ejemplo de salida
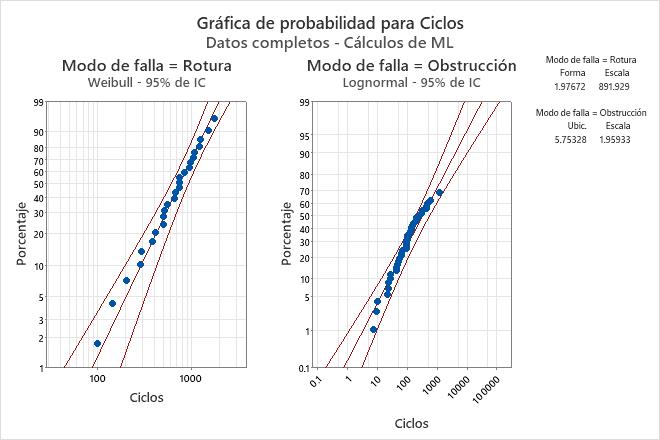
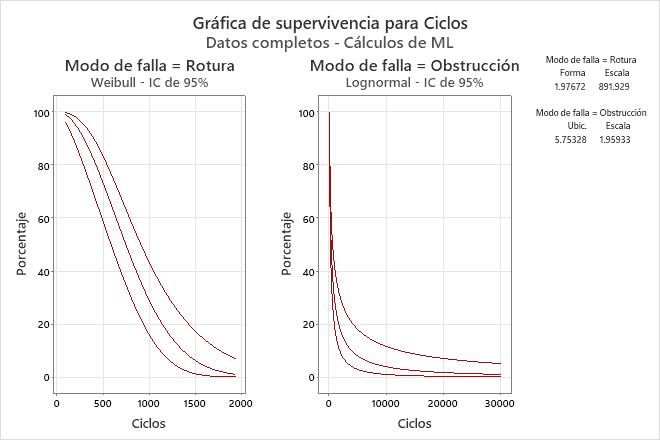
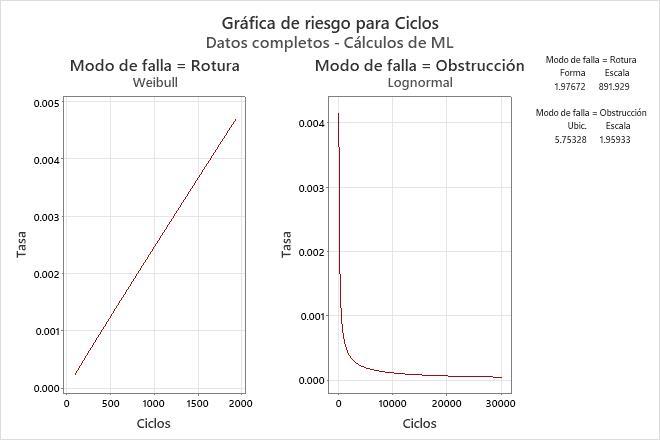
Interpretación
- Forma = 1.97672 y escala = 891.929 para roturas de los brazos rociadores
- Ubicación = 5.75328 y escala = 1.95933 para obstrucciones de los brazos rociadores
La probabilidad que tienen los brazos rociadores de sobrevivir a las roturas en 200 ciclos es de 95% y de sobrevivir a las obstrucciones en 1500 ciclos es de aproximadamente 20%.
La tasa de riesgo para roturas aumenta ligeramente con el tiempo, pero para obstrucciones disminuye en el tiempo.
