Métodos y fórmulas para los métodos de estimación en Análisis de distribución no paramétrico (Censura por la derecha)

El estimador de Kaplan-Meier, también conocido como el estimador del límite del producto, puede utilizarse para calcular probabilidades de supervivencia de conjuntos de datos no paramétricos con múltiples fallas y suspensiones. La ecuación del estimador viene dada por:

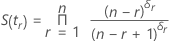
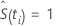
con S(t₀) = 1 y t₀ = 0.

Función de riesgo empírico

La función de riesgo describe la tasa de fallas de un intervalo. La función de riesgo es 0 antes de la primera observación censurada. La función de riesgo cambia solo en observaciones censuradas. Minitab no grafica la función de riesgo después del último punto de datos sin censura.

Cuando hay empates, Minitab utiliza el rango más grande en el empate para estimar la función de riesgo. Para obtener más detalles, vea Nelson¹.

Tiempo promedio para fallar

Para datos sin censura, el tiempo promedio para fallar es igual al tiempo promedio de falla. La fórmula general que se utiliza con datos censurados o sin censura es la siguiente:

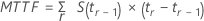
Asimismo, cuando la observación más grande está censurada, Minitab trata el tiempo de la observación más grande sin censura como un límite de tiempo para el cálculo. Para obtener más detalles, vea Lee².

Error estándar of MTTF

El error estándar del tiempo promedio para fallar es la raíz cuadrada de la varianza. Cuando todas las observaciones son sin censura, Minitab calcula una estimación sin sesgo:

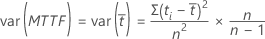
Para los casos en que algunos datos están censurados, la estimación sin sesgo de la varianza utiliza la siguiente fórmula:

Debido a la forma de la función de riesgo empírica, las áreas debajo de la curva de supervivencia, A_r, son rectángulos con altura igual a la función de supervivencia y longitud igual a los intervalos entre observaciones sin censura.

Notación

Término	Description
tr	tiempo del punto de datos con rango r
r	rango del punto de datos donde la primera falla tiene el rango más bajo
n	número total de unidades
δr	0 si la jésima observación está censurada o 1 si la jésima observación está sin censura
c	número de puntos de datos hasta la siguiente observación sin censura
S(tr)	función de supervivencia empírica en el tiempo tr
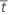	tensión de falla promedio
Ar	área debajo de la curva de la gráfica de supervivencia a la derecha de tr
m	número total de observaciones sin censura

Referencias

1. W. Nelson (1982). Applied Life Data Analysis. John Wiley & Sons, Inc. 133.

2. Elisa T. Lee (1992). Statistical Methods for Survival Data Analysis, Second Edition. John Wiley & Sons, Inc. 73-76.

El modelo actuarial es un análisis no paramétrico alternativo que muestra información para agrupaciones de tiempos de falla. El método de Kaplan-Meier presupone que las suspensiones en un intervalo ocurren al final de ese intervalo, después que han ocurrido las fallas. El método actuarial de Minitab presupone que las suspensiones ocurren en el medio del intervalo, lo cual tiene el efecto de reducir el número de unidades disponibles en el intervalo. La estimación de la función de supervivencia utilizando el método actuarial se realiza de la siguiente forma:

para i = 0

para i > 0

Función de riesgo empírico

La función de riesgo describe la tasa de fallas de un intervalo. Con estimación actuarial, usted presupone que el cálculo es para el punto medio del intervalo. En la gráfica de riesgo, la función se traza de punto medio a punto medio. Para obtener más detalles, vea las referencias después de la sección Notación.

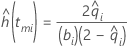
Notación

Término	Description
ni	el número de unidades que ingresan en un intervalo
di	el número que falla en el intervalo
n'i
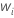	el número censurado en un intervalo
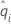	la probabilidad condicional de un evento, que es igual a di/n'i
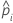tmi	tiempo en el punto medio del intervalo actuarial
bi	la longitud del intervalo actuarial

Referencias

Collett, D. (1994) Modelling Survival Data in Medical Research, Chapman and Hall.

Lee, Elisa T. (1992) Statistical Methods for Survival Data Analysis, 2nd Edition, John Wiley & Sons.

Turnbull^{1, 2} desarrolló un algoritmo iterativo para calcular una estimación no paramétrica de máxima verosimilitud de la función de distribución acumulada de los datos. Este método se aplica a situaciones más generales, por ejemplo, donde los intervalos se sobreponen.

Minitab muestra salida que resume la estimación de Turnbull de las probabilidades de los intervalos, junto con los errores estándar de estas probabilidades.

Referencias

Independientemente del método de estimación, Minitab utiliza una aproximación a la normal para calcular intervalos de confianza. Los intervalos de confianza son los siguientes:

Fórmula

Estimar la probabilidad de supervivencia z_α × Error estándar de la estimación

Notación

Término	Description
zα	la 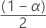valor crítico superior de la distribución normal estándar
α	el nivel de confianza