Un ingeniero especializado en fiabilidad estudia las tasas de fallas de las bobinas de los ensambles de motor para determinar los tiempos en los que fallan las bobinas. A altas temperaturas, las bobinas pueden dañarse demasiado rápido.
El ingeniero registra los tiempos de falla de las bobinas de motor a 80° C y 100° C. Sin embargo, algunas de las unidades deben retirarse de la prueba antes de que fallen. Por lo tanto, los datos están censurados por la derecha. El ingeniero utiliza el Análisis de distribución no paramétrico (Censura porla derecha) para determinar lo siguiente:
- Los tiempos a los cuales fallan diversos porcentajes de las bobinas.
- El porcentaje de bobinas que sobrevive más allá de diversos lapsos de tiempo.
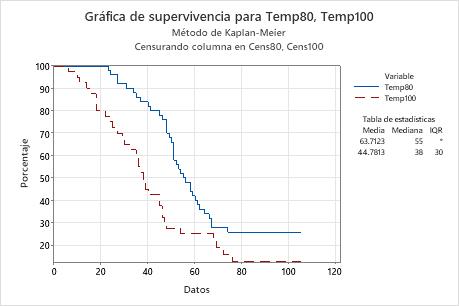
- La función de supervivencia para las bobinas de motor (como se muestra en una gráfica de supervivencia).
- Si las curvas de supervivencia a las dos temperaturas son significativamente diferentes.
- Abra los datos de muestra, FiabilidadDevanadosMotor.MTW.
- Elija .
- En Variables, ingrese Temp80Temp100.
- Haga clic en Censurar. En Usar columnas de censura, ingrese Cens80Cens100.
- En Valor de censura, escriba 0. Haga clic en Aceptar.
- Haga clic en Gráficas. Seleccione Gráfica de supervivencia.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
La mediana de tiempo de falla estimada de Temp80 es 55 horas y la mediana de tiempo de falla estimada de Temp100 es 38. Por lo tanto, el aumento en la temperatura disminuye la mediana de tiempo de falla en aproximadamente 17 horas.
Minitab muestra las estimaciones de supervivencia en la tabla de Estimaciones de Kaplan-Meier. A 80° C, 0.9000 (90%) de las bobinas sobrevive más de 31 horas. A 100° C, 0.9000 (90%) de las bobinas sobrevive más de 14 horas.
En la tabla Estadísticos de prueba, un valor p < α (usualmente, α = 0.05) indica que las curvas de supervivencia son significativamente diferentes. En este caso, los dos valores p (0.005 y 0.000) son menores que α, lo cual sugiere que un cambio de 20° C tiene un efecto en la avería de bobinas de motor.
- 80° C
- Variable: Temp80
Censura
Información de censura Conteo Valor no censurado 37 Valor censurado por la derecha 13 Cálculos no paramétricosCaracterísticas de la variable
Error
estándarIC normal de 95.0% Media(MTTF) Inferior Superior Q1 Mediana Q3 IQR 63.7123 3.83453 56.1968 71.2279 48 55 * * Cálculos de Kaplan-Meier
Número
en
riesgoNúmero
de
fallasProbabilidad de
supervivenciaError
estándarIC normal de 95.0% Tiempo Inferior Superior 23 50 1 0.980000 0.0197990 0.941195 1.00000 24 49 1 0.960000 0.0277128 0.905684 1.00000 27 48 2 0.920000 0.0383667 0.844803 0.99520 31 46 1 0.900000 0.0424264 0.816846 0.98315 34 45 1 0.880000 0.0459565 0.789927 0.97007 35 44 1 0.860000 0.0490714 0.763822 0.95618 37 43 1 0.840000 0.0518459 0.738384 0.94162 40 42 1 0.820000 0.0543323 0.713511 0.92649 41 41 1 0.800000 0.0565685 0.689128 0.91087 45 40 1 0.780000 0.0585833 0.665179 0.89482 46 39 1 0.760000 0.0603987 0.641621 0.87838 48 38 3 0.700000 0.0648074 0.572980 0.82702 49 35 1 0.680000 0.0659697 0.550702 0.80930 50 34 1 0.660000 0.0669925 0.528697 0.79130 51 33 4 0.580000 0.0697997 0.443195 0.71680 52 29 1 0.560000 0.0701997 0.422411 0.69759 53 28 1 0.540000 0.0704840 0.401854 0.67815 54 27 1 0.520000 0.0706541 0.381521 0.65848 55 26 1 0.500000 0.0707107 0.361410 0.63859 56 25 1 0.480000 0.0706541 0.341521 0.61848 58 24 2 0.440000 0.0701997 0.302411 0.57759 59 22 1 0.420000 0.0697997 0.283195 0.55680 60 21 1 0.400000 0.0692820 0.264210 0.53579 61 20 1 0.380000 0.0686440 0.245460 0.51454 62 19 1 0.360000 0.0678823 0.226953 0.49305 64 18 1 0.340000 0.0669925 0.208697 0.47130 66 17 1 0.320000 0.0659697 0.190702 0.44930 67 16 2 0.280000 0.0634980 0.155546 0.40445 74 13 1 0.258462 0.0621592 0.136632 0.38029 - 100° C
- Variable: Temp100
Censura
Información de censura Conteo Valor no censurado 34 Valor censurado por la derecha 6 Cálculos no paramétricosCaracterísticas de la variable
Error
estándarIC normal de 95.0% Media(MTTF) Inferior Superior Q1 Mediana Q3 IQR 44.7813 4.43366 36.0914 53.4711 24 38 54 30 Cálculos de Kaplan-Meier
Número
en
riesgoNúmero
de
fallasProbabilidad de
supervivenciaError
estándarIC normal de 95.0% Tiempo Inferior Superior 6 40 1 0.97500 0.0246855 0.926617 1.00000 10 39 1 0.95000 0.0344601 0.882459 1.00000 11 38 1 0.92500 0.0416458 0.843376 1.00000 14 37 1 0.90000 0.0474342 0.807031 0.99297 16 36 1 0.87500 0.0522913 0.772511 0.97749 18 35 3 0.80000 0.0632456 0.676041 0.92396 22 32 1 0.77500 0.0660256 0.645592 0.90441 24 31 1 0.75000 0.0684653 0.615810 0.88419 25 30 1 0.72500 0.0706001 0.586626 0.86337 27 29 1 0.70000 0.0724569 0.557987 0.84201 29 28 1 0.67500 0.0740566 0.529852 0.82015 30 27 1 0.65000 0.0754155 0.502188 0.79781 32 26 1 0.62500 0.0765466 0.474972 0.77503 35 25 1 0.60000 0.0774597 0.448182 0.75182 36 24 2 0.55000 0.0786607 0.395828 0.70417 37 22 1 0.52500 0.0789581 0.370245 0.67975 38 21 2 0.47500 0.0789581 0.320245 0.62975 39 19 1 0.45000 0.0786607 0.295828 0.60417 40 18 1 0.42500 0.0781625 0.271804 0.57820 45 17 2 0.37500 0.0765466 0.224972 0.52503 46 15 2 0.32500 0.0740566 0.179852 0.47015 47 13 1 0.30000 0.0724569 0.157987 0.44201 48 12 1 0.27500 0.0706001 0.136626 0.41337 54 11 1 0.25000 0.0684653 0.115810 0.38419 68 8 1 0.21875 0.0666585 0.088102 0.34940 69 7 1 0.18750 0.0640434 0.061977 0.31302 72 6 1 0.15625 0.0605154 0.037642 0.27486 76 5 1 0.12500 0.0559017 0.015435 0.23457 - Comparación de curvas de supervivencia
Estadísticas de prueba
Método Chi-cuadrada GL Valor p Clasificación del logaritmo 7.7152 1 0.005 Wilcoxon 13.1326 1 0.000
