En este tema
Estimaciones de parámetros
Fórmula
| Distribución | Parámetros |
|---|---|
|
Valor extremo más pequeño Normal Logística |
μ = ubicación, σ = escala, σ > 0 |
|
Lognormal Loglogística |
μ = ubicación, μ > 0 σ = escala, σ > 0 |
|
Lognormal de 3 parámetros Loglogística de 3 parámetros |
μ = ubicación, μ > 0 σ = escala, σ > 0 λ = valor umbral. |
|
Weibull |
α = escala, α = exp(μ) β = forma, β = 1/σ |
|
Weibull de 3 parámetros |
α = escala, α = exp(μ) β = forma, β = 1/σ λ = valor umbral, |
|
Exponencial |
θ = escala, θ > 0 |
|
Exponencial de 2 parámetros |
θ = escala, θ > 0 λ = valor umbral, |
Error estándar de estimaciones de parámetros
El error estándar es la desviación estándar de la estimación del parámetro. El error estándar proporciona una medida de la variabilidad en cada estimación.
 ,
,  ,
,  ,
,  ,
,  y
y  denota el error estándar de la MLE de μ, σ, α, β, θ y λ. Cada error estándar se calcula como la raíz cuadrada del elemento diagonal adecuado de la inversa de la matriz de información de Fisher.
denota el error estándar de la MLE de μ, σ, α, β, θ y λ. Cada error estándar se calcula como la raíz cuadrada del elemento diagonal adecuado de la inversa de la matriz de información de Fisher.
Límites de confianza para estimaciones de parámetros
Fórmula
| Distribución | Parámetro | Límite de confianza inferior | Límite de confianza superior |
|---|---|---|---|
| Valor extremo más pequeño, normal, logística, lognormal, loglogística | Ubicación, μ |
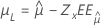 |
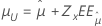 |
| Escala, σ |
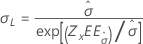 |
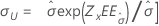 |
|
| lognormal de 3 parámetros, loglogística de 3 parámetros | Ubicación, μ |
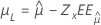 |
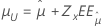 |
| Escala, σ |
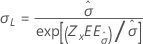 |
 |
|
| Valor umbral, λ |
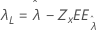 |
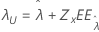 |
|
| Weibull | Forma, β |
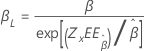 |
 |
| Escala, α |
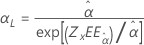 |
 |
|
|
Weibull de 3 parámetros |
Forma, β |
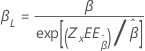 |
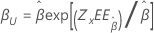 |
|
Escala, α |
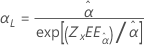 |
 |
|
|
Valor umbral, λ |
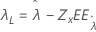 |
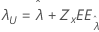 |
|
| Exponencial | Escala |
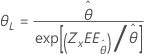 |
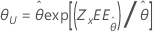 |
| Exponencial de 2 parámetros | Escala, θ |
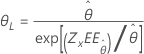 |
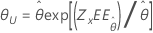 |
| Valor umbral, λ |
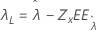 |
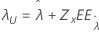 |
Nota
Para algunos datos, la función de probabilidad no tiene bordes y, por lo tanto, genera estimaciones poco uniformes para distribuciones con un parámetro umbral (como la exponencial de 2 parámetros). Cuando esto ocurre, la matriz de varianzas y covarianzas de los parámetros estimados no se puede determinar numéricamente. En ese caso, Minitab presupone que 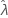 está fijado, lo que produce un EE (
está fijado, lo que produce un EE (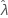 ) = 0. El borde superior e inferior de
) = 0. El borde superior e inferior de 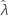 es
es 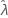 .
.
Notación
| Término | Description |
|---|---|
| zx | la  valor crítico superior de la distribución normal estándar, donde 100x % es el nivel de confianza y 0 < x < 1. valor crítico superior de la distribución normal estándar, donde 100x % es el nivel de confianza y 0 < x < 1. |




