Utilice la gráfica de probabilidad para comparar los ajustes de distribuciones comunes a fin de elegir la distribución de mejor ajuste. Si los puntos de datos se sitúan a lo largo de una línea relativamente recta en la gráfica de probabilidad, entonces usted puede concluir que es razonable modelar sus datos utilizando esa distribución. Por lo tanto, la distribución de mejor ajuste es aquella en la cual los puntos siguen más de cerca la línea ajustada.
Los puntos en la gráfica son los percentiles estimados de las fallas basados en un método no paramétrico. Cuando usted detiene el cursor en un punto de datos, Minitab muestra el tiempo de falla observado y la probabilidad acumulada estimada.
La línea se basa en la distribución ajustada. En este ejemplo, Weibull, lognormal, exponencial y normal son las distribuciones ajustadas. Cuando usted detiene el cursor en la línea ajustada, Minitab muestra una tabla de percentiles de varios porcentajes.
Para el método de estimación de máxima verosimilitud (MLE), Minitab muestra el estadístico de Anderson-Darling (ajust.) para evaluar el ajuste de cada distribución.
Cuando usted utiliza el método de estimación de mínimos cuadrados (LSXY), Minitab muestra el coeficiente de correlación de Pearson, el cual es un número positivo que no puede ser mayor que 1. Valores de coeficientes de correlación más altos indican que la distribución provee un mejor ajuste.
Nota
Para obtener más información sobre interpretación del estadístico de Anderson-Darling (ajust.), vaya a "Bondad de ajuste".
Ejemplo de salida
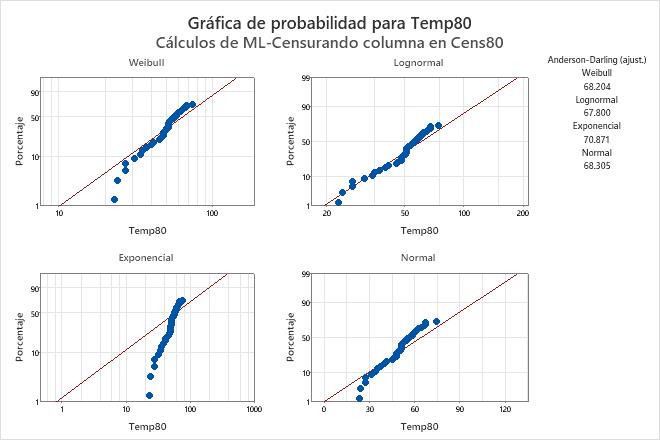
Interpretación
Para los datos sobre bobinas de motor, las gráficas de probabilidad muestran que la distribución de Weibull y la distribución lognormal ajustan los datos mucho más que la distribución exponencial o la distribución normal. La distribución lognormal parece proveer el mejor ajuste a estos datos.
