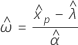Percentiles y errores estándar de percentiles
Los percentiles son estimaciones de los tiempos en los cuales cierto porcentaje de la población ha fallado. Por opción predeterminada, Minitab muestra tablas de percentiles para el análisis de distribución paramétrico de percentiles comunes.
Los errores estándar de las estimaciones de percentiles son la raíz cuadrada de las varianzas.
 ,
,  ,
,  ,
,  ,
,  ,
, 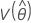 ,
, 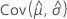 ,
, 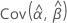 ,
, 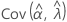 ,
, 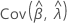 ,
, 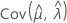 y
y 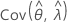 denota las varianzas y covarianzas de las MLE de μ, σ, α, β, θ y λ, que se toman del elemento adecuado de la inversa de la matriz de información de Fisher.
denota las varianzas y covarianzas de las MLE de μ, σ, α, β, θ y λ, que se toman del elemento adecuado de la inversa de la matriz de información de Fisher.
Las fórmulas utilizadas para estimaciones de percentiles y varianzas para cada distribución son las siguientes:
Valor extremo más pequeño
- Percentil
-
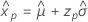
- Varianza
-
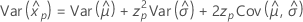
Weibull
- Percentil
-

- Varianza
-
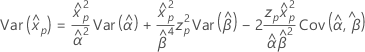
Weibull de 3 parámetros
- Percentil
-

- Varianza
-
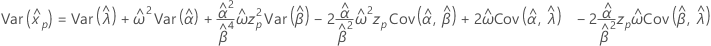
Exponencial
- Percentil
-

- Varianza
-

Exponencial de 2 parámetros
- Percentil
-

- Varianza
-
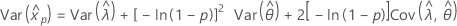
Normal
- Percentil
-
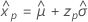
- Varianza
-
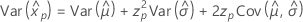
Lognormal
- Percentil
-

- Varianza
-
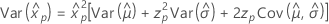
Lognormal de 3 parámetros
- Percentil
-

- Varianza
-
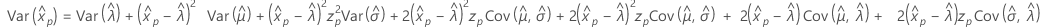
Logística
- Percentil
-
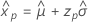
- Varianza
-
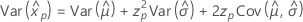
Loglogística
- Percentil
-
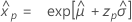
- Varianza
-
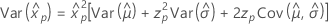
Loglogística de 3 parámetros
- Percentil
-

- Varianza
-

Notación
| Término | Description |
|---|---|
| zp |
la cdf inversa de la distribución estándar evaluada en p (el percentil pésimo de la distribución estándar) |
Límites de confianza para percentiles
| Distribución | Límites de confianza |
|---|---|
|
Valor extremo más pequeño Normal Logística |
  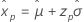 |
|
Weibull Exponencial Lognormal Loglogística |
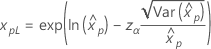 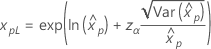 donde |
|
Weibull de 3 parámetros Exponencial de 2 parámetros Lognormal de 3 parámetros Loglogística de 3 parámetros |
Si λ < 0:   Si λ 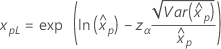 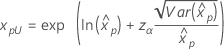 donde |
Para los cálculos de la varianza de xp estimada, vea la sección "Percentiles y error estándar de percentiles".
Notación
| Término | Description |
|---|---|
| zα | la 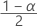 valor crítico superior de la distribución normal estándar, donde 100α % es el nivel de confianza. valor crítico superior de la distribución normal estándar, donde 100α % es el nivel de confianza. |