Un ingeniero especializado en fiabilidad desea evaluar la fiabilidad de un nuevo tipo de silenciador y estimar la proporción de reclamos de garantía que se pueden esperar con una garantía de 50,000 millas. El ingeniero recopila datos de fallas sobre ambos tipos de silenciadores: los antiguos y los nuevos. Los silenciadores fueron inspeccionados para detectar fallas cada 10,000 millas.
El ingeniero registra el número de fallas por cada intervalo de 10,000 millas. Por lo tanto, los datos están censurados arbitrariamente. Antes de analizar los datos de fallas de los silenciadores nuevos utilizando el Análisis de distribución paramétrico (Censura arbitraria), el ingeniero utiliza la Gráfica de ID de distribución (Censura arbitraria) para seleccionar un modelo de distribución para el análisis.
- Abra los datos de muestra, FiabilidadSilenc.MWX.
- Elija .
- En Variables iniciales, ingrese InicioNuevo.
- En Variables finales, ingrese FinNuevo.
- En Columnas de frecuencia (opcional), ingrese FrecNuevo.
- Seleccione Especificar. Asegúrese de que las distribuciones predeterminadas estén seleccionadas (Weibull, Lognormal, Exponencial y Normal).
- Haga clic en Aceptar.
Interpretar los resultados
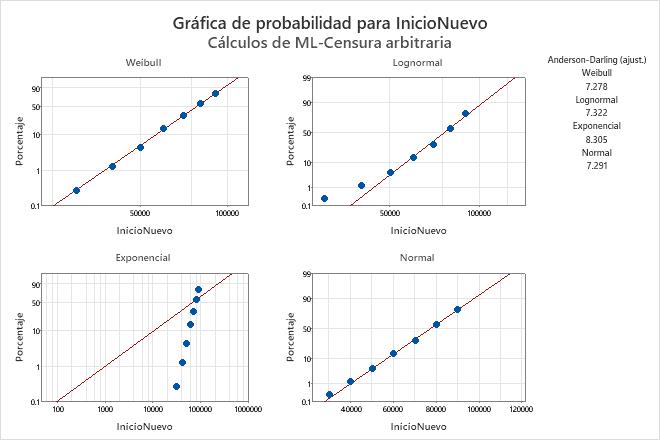
En la gráfica de probabilidad de Weibull, los puntos se ubican aproximadamente en la línea recta. Por lo tanto, la distribución de Weibull provee un ajuste adecuado. Por lo tanto, el ingeniero decide utilizar la distribución de Weibull para modelar los datos para Análisis de distribución paramétrico (censura arbitraria).
Minitab también muestra una tabla de percentiles y una tabla de tiempo promedio para fallar (MTTF), que provee tiempos de falla calculados para cada distribución. Usted puede comparar los valores calculados para ver cómo sus conclusiones pueden cambiar con diferentes distribuciones. Si varias distribuciones ajustan sus datos adecuadamente, le convendría utilizar la distribución que proporcione los resultados más conservadores.
Bondad de ajuste
| Distribución | Anderson-Darling (ajust.) |
|---|---|
| Weibull | 7.278 |
| Lognormal | 7.322 |
| Exponencial | 8.305 |
| Normal | 7.291 |
Tabla de percentiles
| Error estándar | IC normal de 95% | ||||
|---|---|---|---|---|---|
| Distribución | Porcentaje | Percentil | Inferior | Superior | |
| Weibull | 1 | 37265.1 | 938.485 | 35470.3 | 39150.6 |
| Lognormal | 1 | 43817.7 | 688.033 | 42489.7 | 45187.2 |
| Exponencial | 1 | 941.789 | 32.5296 | 880.143 | 1007.75 |
| Normal | 1 | 39810.3 | 1047.34 | 37757.6 | 41863.1 |
| Weibull | 5 | 49434.9 | 841.147 | 47813.5 | 51111.3 |
| Lognormal | 5 | 51458.9 | 624.451 | 50249.5 | 52697.5 |
| Exponencial | 5 | 4806.55 | 166.019 | 4491.93 | 5143.21 |
| Normal | 5 | 50694.9 | 810.524 | 49106.3 | 52283.5 |
| Weibull | 10 | 56006.1 | 759.186 | 54537.7 | 57514.0 |
| Lognormal | 10 | 56063.1 | 585.905 | 54926.4 | 57223.3 |
| Exponencial | 10 | 9873.05 | 341.017 | 9226.79 | 10564.6 |
| Normal | 10 | 56497.5 | 699.183 | 55127.1 | 57867.8 |
| Weibull | 50 | 77639.9 | 501.312 | 76663.5 | 78628.7 |
| Lognormal | 50 | 75850.3 | 576.625 | 74728.5 | 76988.9 |
| Exponencial | 50 | 64952.9 | 2243.49 | 60701.3 | 69502.3 |
| Normal | 50 | 76966.0 | 514.756 | 75957.1 | 77974.9 |
Tabla de MTTF
| Error estándar | IC normal de 95% | |||
|---|---|---|---|---|
| Distribución | Media | Inferior | Superior | |
| Weibull | 76585.0 | 488.71 | 75633.1 | 77549 |
| Lognormal | 77989.9 | 615.96 | 76792.0 | 79207 |
| Exponencial | 93707.3 | 3236.67 | 87573.5 | 100271 |
| Normal | 76966.0 | 514.76 | 75957.1 | 77975 |
