Se provee fiabilidad
Si usted especifica la meta de fiabilidad en términos de un tiempo y una fiabilidad, Minitab primero calcula el parámetro que se demostrará utilizando la fórmula de la distribución especificada en la siguiente tabla.
Luego, Minitab calcula el tiempo de pruebas o el tamaño de la muestra de la misma manera que en el caso de las pruebas de sustentación.
| Distribución (parámetro) | Parámetro que se demostrará |
|---|---|
| Weibull (escala) |
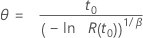 |
| Exponencial (media) |
 |
|
Valor extremo más pequeño (ubicación) Normal (media) Logística (media) |
 |
|
Lognormal (ubicación logarítmica) Loglogística (ubicación logarítmica) |
 |
Notación
| Término | Description |
|---|---|
| t | tiempo |
| R(t) | función de fiabilidad |
| θ | escala (Weibull) o media (exponencial) |
| β | parámetro de forma (Weibull) |
| σ | parámetro de escala (lognormal, loglogística, logística, normal, valor extremo más pequeño) |
| μ | media (normal, logística) o ubicación logarítmica (lognormal, loglogística) |
| Φ-1 | CDF inversa para la distribución correspondiente |
Se provee el percentil P ésimo
Si usted especifica la meta de fiabilidad en términos del percentil Pésimo (tp), Minitab primero calcula el parámetro que se demostrará utilizando la fórmula de la distribución especificada en la siguiente tabla.
Luego, Minitab calcula el tiempo de pruebas o el tamaño de la muestra de la misma manera que en el caso de las pruebas de sustentación.
| Distribución (parámetro) | Parámetro que se demostrará |
|---|---|
| Weibull (escala) |
 |
| Exponencial (media) |
 |
|
Valor extremo más pequeño (ubicación) Normal (media) Logística (media) |
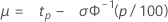 |
|
Lognormal (ubicación logarítmica) Loglogística (ubicación logarítmica) |
 |
Notación
| Término | Description |
|---|---|
| t | tiempo |
| R(t) | función de fiabilidad |
| p | percentil |
| α | escala (Weibull) |
| θ | media (exponencial) |
| μ | media (normal, logística), ubicación (valor extremo más pequeño) o ubicación logarítmica (lognormal, loglogística) |
| Φ-1 | CDF inversa para la distribución correspondiente |
Se provee MTTF
Si usted especifica la meta de fiabilidad en términos del MTTF, Minitab primero calcula el parámetro que se demostrará utilizando la fórmula de la distribución especificada en la siguiente tabla.
Luego, Minitab calcula el tiempo de pruebas o el tamaño de la muestra de la misma manera que en el caso de las pruebas de sustentación
| Distribución (parámetro) | Parámetro que se demostrará |
|---|---|
| Weibull (escala) |
 |
| Exponencial (media) |
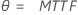 |
|
Normal (media) Logística (media) |
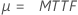 |
|
Lognormal (ubicación logarítmica) |
 |
|
Loglogística (ubicación logarítmica) |
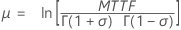 |
|
Valor extremo más pequeño (ubicación) |
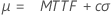 |
Notación
| Término | Description |
|---|---|
| α | escala (Weibull) |
| σ | escala (lognormal, loglogística, valor extremo más pequeño) |
| β | forma (Weibull) |
| θ | media (exponencial) |
| μ | media (normal, logística), ubicación (valor extremo más pequeño) o ubicación logarítmica (lognormal, loglogística) |
| MTTF | tiempo promedio para fallar |
| c | Constante de Euler ≈ 0.5772 |
| Γ | función gamma |
