Funciones de fiabilidad y fiabilidad inversa
Valor extremo más pequeño
- Fiabilidad
-

- Fiabilidad inversa
-

donde
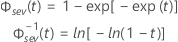
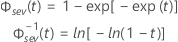
| Término | Description |
|---|---|
| t | tiempo |
| μ | parámetro de ubicación |
| σ | parámetro de escala |
| Φsev(t) | CDF de la distribución de valor extremo más pequeño |
| Φ-1sev(t) | CDF inversa de la distribución de valor extremo más pequeño |
Weibull
- Fiabilidad
-
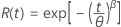
- Fiabilidad inversa
-

| Término | Description |
|---|---|
| t | tiempo |
| p | probabilidad |
| β | parámetro de forma |
| θ | parámetro de escala |
Exponencial
- Fiabilidad
-

- Fiabilidad inversa
-
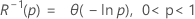
| Término | Description |
|---|---|
| t | tiempo |
| p | probabilidad |
| θ | Parámetro de media |
Normal
- Fiabilidad
-
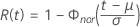
- Fiabilidad inversa
-

| Término | Description |
|---|---|
| t | tiempo |
| μ | parámetro de ubicación |
| σ | parámetro de escala |
| Φnor(t) | CDF de la distribución normal |
| Φ-1nor(t) | CDF inversa de la distribución normal |
Lognormal
- Fiabilidad
-

- Fiabilidad inversa
-
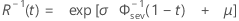
| Término | Description |
|---|---|
| t | tiempo |
| μ | parámetro de ubicación |
| σ | parámetro de escala |
| Φnor(t) | CDF de la distribución normal |
| Φ-1nor(t) | CDF inversa de la distribución normal |
Logística
- Fiabilidad
-
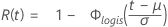
- Fiabilidad inversa
-
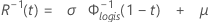
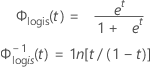
| Término | Description |
|---|---|
| t | tiempo |
| μ | parámetro de ubicación |
| σ | parámetro de escala |
| Φlogis(t) | CDF de la distribución logística |
| Φ-1logis(t) | CDF inversa de la distribución logística |
Loglogística
- Fiabilidad
-

- Fiabilidad inversa
-
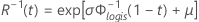
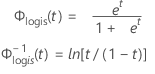
| Término | Description |
|---|---|
| t | tiempo |
| μ | parámetro de ubicación |
| σ | parámetro de escala |
| Φlogis(t) | CDF de la distribución logística |
| Φ-1logis(t) | CDF inversa de la distribución logística |
Ecuación
La ecuación para un plan de pruebas de m fallas es la siguiente:

Notación
| Término | Description |
|---|---|
| α | alfa (que es igual a 1 – el nivel de confianza) |
| R | función de fiabilidad o supervivencia en el tiempo t |
| N | número mínimo de unidades que se probarán |
