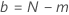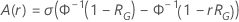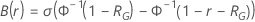Los cálculos de la probabilidad de pasar un plan de pruebas dependen de la distribución que modela las fallas. Para una distribución logarítmica-ubicación-escala, la probabilidad depende de la relación de mejora. Para una distribución de ubicación-escala, la probabilidad depende de la cantidad de mejora. La expresión de las fórmulas se divide perfectamente en dos casos que dependen de si se especifica el tamaño de la muestra o el tiempo de prueba.
Tamaño de la muestra
Cuando las especificaciones de una prueba de demostración incluyen el tamaño de la muestra, los cálculos de la probabilidad de pasar requieren el tiempo de prueba. Para un tamaño de muestra determinado, el tiempo de prueba para un nivel de confianza de satisface la siguiente ecuación:
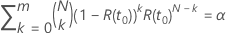
Para un punto en el tiempo, , la solución es, , de la ecuación tiene la siguiente forma:
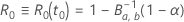
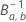donde es la función de distribución acumulada inversa de la distribución beta con los siguientes parámetros de forma:
Para calcular , invierta la función . La inversión depende de la familia de distribuciones.
Familia logarítmica-ubicación-escala
Familia ubicación-escala
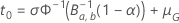
La probabilidad de pasar la prueba tiene la siguiente forma que depende de y la mejora:
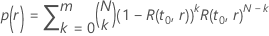
donde 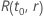es la función de fiabilidad del modelo de distribución en términos de y .
La función de fiabilidad depende de la familia de distribuciones:
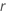Familia logarítmica-ubicación-escala
Familia ubicación-escala
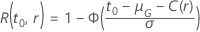
La tabla siguiente da la función de para la familia de distribuciones y la meta de la prueba:
Meta de fiabilidad
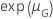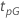Logarítmica-ubicación-escala
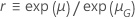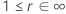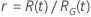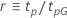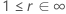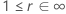Meta de fiabilidad
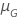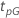Ubicación-escala
donde
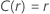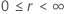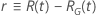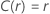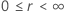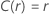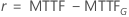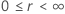Ejemplo de 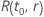para la distribución de Weibull
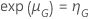Para un plan de pruebas con la distribución Weibull, una meta de fiabilidad de , y un tamaño de muestra determinado, la probabilidad de pasar tiene la siguiente forma:
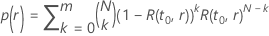
donde
Tiempo de prueba
Cuando las especificaciones de una prueba de demostración incluyen el tiempo de prueba, los cálculos de la probabilidad de pasar requieren el tamaño de la muestra. Para un tiempo de prueba determinado, el tamaño de la muestra para un nivel de confianza de satisface la siguiente ecuación:
Para un plan de pruebas de 0 fallas (), la solución de la ecuación, 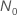, tiene la siguiente forma:
.
Para un plan de pruebas con fallas (), no existe ninguna solución de forma cerrada. Meeker y Escobar (1998)1 da la siguiente solución aproximada:
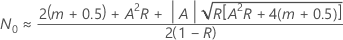
donde
Minitab encuentra la solución exacta numéricamente cuando .
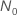La probabilidad de pasar la prueba tiene la siguiente forma que depende de y la mejora:
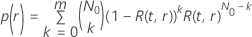
donde 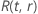es la función de fiabilidad del modelo de distribución en términos de y .
La función de fiabilidad depende de la familia de distribuciones:
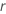Familia logarítmica-ubicación-escala
Familia ubicación-escala
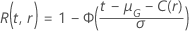
La función tiene las mismas definiciones que cuando las especificaciones de la prueba dan el tamaño de la muestra.
Ejemplo de 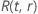para la distribución de Weibull
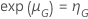Para un plan de pruebas con la distribución de Weibull, una meta de fiabilidad de y un tiempo de prueba determinado, la probabilidad de pasar tiene la siguiente forma:
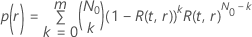
donde
Notación
Término
Description
N
tamaño de la muestra para el diseño cuando las especificaciones de la prueba proporcionan el tamaño de la muestra
m
número de unidades que fallan durante la prueba
nivel de significancia, de modo que el nivel de confianza de la prueba de demostración sea
parámetro de escala
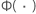función de distribución acumulada de la distribución estándar para la distribución logarítmica-ubicación-escala o la distribución de ubicación-escala seleccionada
función de distribución acumulada inversa de la distribución estándar para la distribución logarítmica-ubicación-escala o la distribución de ubicación-escala seleccionada
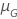parámetro de ubicación para la distribución que cumple con la meta de la prueba
parámetro de forma de la distribución de Weibull
tiempo de prueba cuando las especificaciones de la prueba proporcionan el tamaño de la muestra
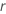relación de mejora de las distribuciones logarítmica-ubicación-escala o la cantidad de mejora para las distribuciones de ubicación-escala
fiabilidad en el tiempo t que es la meta de la prueba
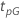percentil en el porcentaje p que es la meta de la prueba
tiempo medio antes de falla que es la meta de la prueba
tiempo de prueba cuando las especificaciones de la prueba proporcionan el tiempo de prueba
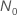tamaño de la muestra cuando las especificaciones de la prueba proporcionan el tiempo de prueba
1 W. Q. Meeker y L. A. Escobar (1998). Statistical Methods for Reliability Data. Wiley, New York.
satisface la siguiente ecuación:
, la solución es, 
, de la ecuación tiene la siguiente forma:
es la función de distribución acumulada inversa de la distribución beta con los siguientes parámetros de forma:
, invierta la función 
. La inversión depende de la familia de distribuciones.
y la mejora:
es la función de fiabilidad del modelo de distribución en términos de 
y 
.
para la familia de distribuciones y la meta de la prueba:
para la distribución de Weibull
, y un tamaño de muestra determinado, la probabilidad de pasar tiene la siguiente forma:
satisface la siguiente ecuación:
), la solución de la ecuación, 
, tiene la siguiente forma:
), no existe ninguna solución de forma cerrada. Meeker y Escobar (1998)1 da la siguiente solución aproximada:
.
y la mejora:
es la función de fiabilidad del modelo de distribución en términos de 
y 
.
tiene las mismas definiciones que cuando las especificaciones de la prueba dan el tamaño de la muestra.
para la distribución de Weibull
y un tiempo de prueba determinado, la probabilidad de pasar tiene la siguiente forma:
