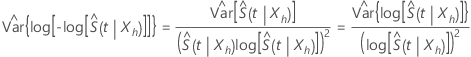En este tema
Función de supervivencia
La función de supervivencia utiliza las siguientes definiciones:
| Término | Description |
|---|---|
 | los tiempos de eventos, distintos, ordenados |
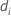 | el número de eventos al tiempo 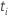 |
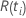 | el riesgo establecido al tiempo 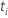 , que es el conjunto de todas las unidades de muestra que aún pueden fallar antes del tiempo , que es el conjunto de todas las unidades de muestra que aún pueden fallar antes del tiempo 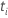 |
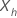 | el vector del componente p de valores covariables que representa un nuevo punto de datos o uno existente |
Dado que 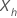 , la función de supervivencia para el modelo de riesgos proporcionales de Cox se expresa de la siguiente forma:
, la función de supervivencia para el modelo de riesgos proporcionales de Cox se expresa de la siguiente forma:
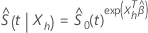
donde

y

La función 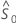 estima la función de supervivencia de un individuo cuando los valores de todas las covariables son 0. La función
estima la función de supervivencia de un individuo cuando los valores de todas las covariables son 0. La función  es el estimador de Breslow de la tasa de riesgo acumulado inicial. La función
es el estimador de Breslow de la tasa de riesgo acumulado inicial. La función  es una función escalonada que aparece en los tiempos del observado.
es una función escalonada que aparece en los tiempos del observado.
Intervalos de confianza
En condiciones de regularidad leve, el estimador 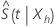 presenta una distribución normal asíntota con media
presenta una distribución normal asíntota con media  y varianza asíntota con la siguiente forma:
y varianza asíntota con la siguiente forma:
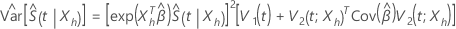
donde

y
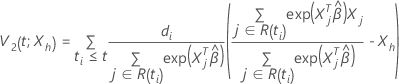
Está disponible un intervalo de confianza del método de Wald directo, pero es menos preciso porque la distribución de 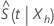 está severamente sesgada. Además, los límites de confianza de dichos intervalos a menudo están fuera del intervalo [0, 1]. La distribución del logaritmo de
está severamente sesgada. Además, los límites de confianza de dichos intervalos a menudo están fuera del intervalo [0, 1]. La distribución del logaritmo de 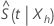 está menos sesgada y converge con más rapidez con la distribución normal. Minitab utiliza las siguientes transformaciones para calcular los intervalos de confianza.
está menos sesgada y converge con más rapidez con la distribución normal. Minitab utiliza las siguientes transformaciones para calcular los intervalos de confianza.
Transformación logarítmica
Minitab calcula un intervalo de confianza para  y vuelve a transformar los límites de confianza para generar el intervalo de confianza de
y vuelve a transformar los límites de confianza para generar el intervalo de confianza de 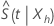 . Utilizando este enfoque, un intervalo de confianza aproximado de 100(1 – α) para
. Utilizando este enfoque, un intervalo de confianza aproximado de 100(1 – α) para 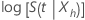 , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
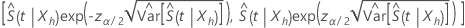
donde  estima la varianza asíntota de
estima la varianza asíntota de  y se expresa de la siguiente forma:
y se expresa de la siguiente forma:
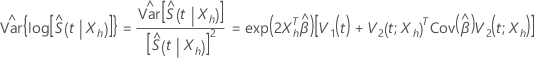
Si el límite de confianza superior de 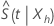 excede 1, entonces Minitab utiliza 1 como límite superior.
excede 1, entonces Minitab utiliza 1 como límite superior.
Transformación log-log
La transformación log-log garantiza que el intervalo de confianza de 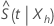 se encuentra en el intervalo (0, 1). Minitab calcula un intervalo de confianza para
se encuentra en el intervalo (0, 1). Minitab calcula un intervalo de confianza para  y vuelve a transformar los límites de confianza para generar el intervalo de confianza de
y vuelve a transformar los límites de confianza para generar el intervalo de confianza de 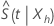 . Utilizando este método, un intervalo de confianza aproximado de 100(1 – α) para
. Utilizando este método, un intervalo de confianza aproximado de 100(1 – α) para  , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
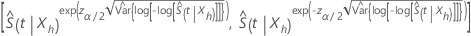
donde 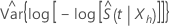 estima la varianza asíntota de
estima la varianza asíntota de  y se expresa de la siguiente forma:
y se expresa de la siguiente forma: