En este tema
Las pruebas de bondad de ajuste evalúan la hipótesis nula 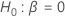 en comparación con la hipótesis alternativa
en comparación con la hipótesis alternativa 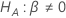 . Para las pruebas,
. Para las pruebas,  es un vector del componente p.
es un vector del componente p.
- Pruebas globales de Wald
- Pruebas globales de relación de verosimilitud
- Pruebas globales de puntuación
En un análisis con conglomerados, Minitab no proporciona las pruebas globales de relación de verosimilitud porque la prueba asume que las observaciones al interior de los conglomerados son independientes.
DF
Los grados de libertad para las pruebas de bondad de ajuste son la suma de los grados de libertad para los términos del modelo. Esta suma equivale al número de parámetros incluidos en el modelo.
Xi cuadrada
El cálculo de la estadística de xi cuadrada depende de la prueba. Cuando la variable de respuesta no tiene tiempos de respuesta empatados, entonces la prueba de puntuación es idéntica a la bien conocida prueba de rangos logarítmicos.
Bajo la hipótesis nula, la estadística de prueba para cada tipo de prueba tiene una distribución asíntota de xi cuadrada. La distribución asíntota es válida cuando el número de eventos observados es grande en comparación con el número de parámetros del modelo. Para los predictores categóricos, el número de eventos en cada nivel también debe ser lo suficientemente grande.
Prueba de relación de verosimilitud
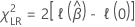
donde 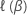 es la función de verosimilitud logarítmica parcial del modelo apropiado.
es la función de verosimilitud logarítmica parcial del modelo apropiado.
Prueba de Wald
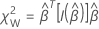
donde 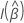 es la matriz de información de Fisher.
es la matriz de información de Fisher.
 la matriz de residuos de puntuación. Entonces, la matriz robusta de varianza y covarianza se expresa de la siguiente forma:
la matriz de residuos de puntuación. Entonces, la matriz robusta de varianza y covarianza se expresa de la siguiente forma:

donde 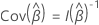 y
y  es la matriz de residuos de puntuación con vista contraída. Para obtener la matriz de residuos de puntuación con vista contraída, sustituya todos los conglomerados de filas de residuos de puntuación con la suma de esas filas de residuos.
es la matriz de residuos de puntuación con vista contraída. Para obtener la matriz de residuos de puntuación con vista contraída, sustituya todos los conglomerados de filas de residuos de puntuación con la suma de esas filas de residuos.

Prueba de puntuación
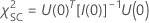
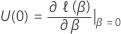
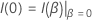

donde  es la matriz de residuos de puntuación con vista contraída para
es la matriz de residuos de puntuación con vista contraída para  . Para obtener la matriz de residuos de puntuación con vista contraída, sustituya todos los conglomerados de filas de residuos de puntuación con la suma de esas filas de residuos.
. Para obtener la matriz de residuos de puntuación con vista contraída, sustituya todos los conglomerados de filas de residuos de puntuación con la suma de esas filas de residuos.
Valor p
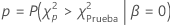
donde  es una variable aleatoria que sigue una distribución de xi cuadrada con
es una variable aleatoria que sigue una distribución de xi cuadrada con  grados de libertad.
grados de libertad.  es la estadística de prueba.
es la estadística de prueba.
