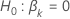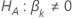Ecuación de regresión
El modelo semiparamétrico de riesgos proporcionales de Cox utiliza los valores predictivos para un individuo, 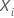 , para predecir la puntuación de riesgo,
, para predecir la puntuación de riesgo, 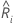 . La ecuación se expresa de la siguiente forma general:
. La ecuación se expresa de la siguiente forma general:

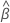 es el vector de los coeficientes estimados. Los coeficientes estimados pueden incluir valores para términos de orden superior, como son los cuadrados de los predictores continuos. La puntuación de riesgo estimada es válida para el periodo de estudio completo y no depende del tiempo. En el resultado, la ecuación se expresa de la siguiente forma, donde aparece una ecuación independiente para los diferentes niveles de factores categóricos:
es el vector de los coeficientes estimados. Los coeficientes estimados pueden incluir valores para términos de orden superior, como son los cuadrados de los predictores continuos. La puntuación de riesgo estimada es válida para el periodo de estudio completo y no depende del tiempo. En el resultado, la ecuación se expresa de la siguiente forma, donde aparece una ecuación independiente para los diferentes niveles de factores categóricos:
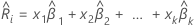
Coef
Sea la función de verosimilitud logarítmica parcial para el modelo de riesgos proporcionales de Cox 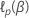 . El vector que maximiza la función de verosimilitud parcial,
. El vector que maximiza la función de verosimilitud parcial, 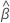 , proporciona los coeficientes estimados para el modelo. Para buscar
, proporciona los coeficientes estimados para el modelo. Para buscar 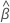 , establezca las derivadas parciales de la función de verosimilitud logarítmica-parcial igual a cero y resuelva las ecuaciones para
, establezca las derivadas parciales de la función de verosimilitud logarítmica-parcial igual a cero y resuelva las ecuaciones para  . Minitab Statistical Software utiliza el método de iteración de Newton-Raphson para resolver las ecuaciones. Consulte Murray (1972)1 for a description of the Newton-Raphson iterative method.
. Minitab Statistical Software utiliza el método de iteración de Newton-Raphson para resolver las ecuaciones. Consulte Murray (1972)1 for a description of the Newton-Raphson iterative method.
El vector de las derivadas parciales de la función de verosimilitud logarítmica parcial depende de que la variable de respuesta incluya eventos con tiempos empatados. Si la variable de respuesta incluye empates, la estimación utiliza la aproximación de Efron o la aproximación de Breslow. Si la variable de respuesta no incluye empates, los 3 métodos proporcionan las mismas estimaciones. Cuantos menos empates existan en los datos, más cercanos serán los resultados de los dos métodos de aproximación. Cuantos más empates existan en los datos, mejor será la aproximación de Efron en comparación con la aproximación de Breslow.
| Término | Description |
|---|---|
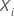 | el vector de valores covariables que corresponde a la unidad de muestra con el tiempo de evento 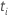 |
Datos sin empates
| Término | Description |
|---|---|
 | el número de tiempos del evento |
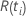 | el riesgo establecido al tiempo 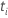 , que es el conjunto de todas las unidades de muestra que aún pueden fallar antes del tiempo , que es el conjunto de todas las unidades de muestra que aún pueden fallar antes del tiempo 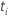 |
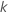 | una variable de conteo para el número de parámetros del modelo,  donde donde  es el número de parámetros del modelo es el número de parámetros del modelo |
La función de verosimilitud parcial para el modelo de riesgos proporcionales de Cox sin empates se expresa de la siguiente forma:
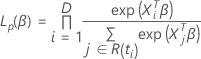
La función de verosimilitud logarítmica parcial se expresa de la siguiente forma:
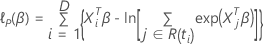
 , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
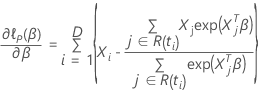
de modo que la derivada parcial para un coeficiente particular, 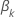 , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
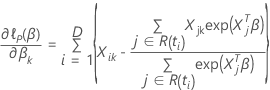
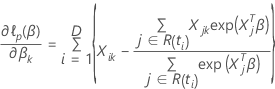
Datos con empates
| Término | Description |
|---|---|
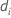 | el número de eventos al tiempo 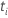 |
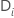 | el conjunto de todas las unidades de muestra con evento al tiempo 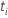 |
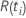 | el riesgo establecido al tiempo 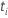 , que es el conjunto de todas las unidades de muestra que aún pueden fallar antes del tiempo , que es el conjunto de todas las unidades de muestra que aún pueden fallar antes del tiempo 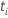 |

Aproximación de Efron para datos con empates
La función de verosimilitud parcial aproximada se expresa de la siguiente forma:
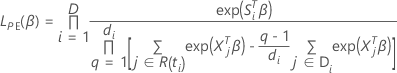
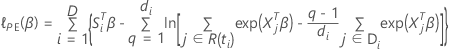
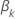 , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
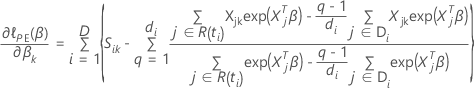
Aproximación de Breslow para datos con empates
La función de verosimilitud parcial aproximada se expresa de la siguiente forma:
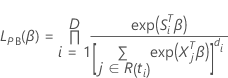
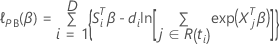
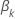 , se expresa de la siguiente forma:
, se expresa de la siguiente forma:
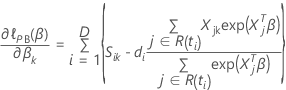
Coeficientes codificados
La tabla muestra coeficientes codificados cuando el análisis estandariza los predictores continuos. Para encontrar los coeficientes codificados, sustituya los predictores estandarizados en las ecuaciones anteriores.
EE del coeficiente
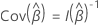
donde la matriz de información observada,  depende de que la variable de respuesta incluya eventos con tiempos empatados. Si la variable de respuesta incluye empates, la estimación utiliza la aproximación de Efron o la aproximación de Breslow. Si la variable de respuesta no incluye empates, los 3 métodos proporcionan las mismas estimaciones. Cuantos menos empates existan en los datos, más cercanos serán los resultados de los dos métodos de aproximación. Cuantos más empates existan en los datos, mejor será la aproximación de Efron en comparación con la aproximación de Breslow.
depende de que la variable de respuesta incluya eventos con tiempos empatados. Si la variable de respuesta incluye empates, la estimación utiliza la aproximación de Efron o la aproximación de Breslow. Si la variable de respuesta no incluye empates, los 3 métodos proporcionan las mismas estimaciones. Cuantos menos empates existan en los datos, más cercanos serán los resultados de los dos métodos de aproximación. Cuantos más empates existan en los datos, mejor será la aproximación de Efron en comparación con la aproximación de Breslow.
Datos sin empates
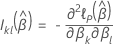
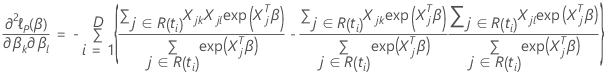
Aproximación de Efron para datos con empates
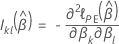
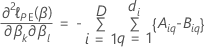
donde
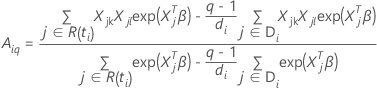
y
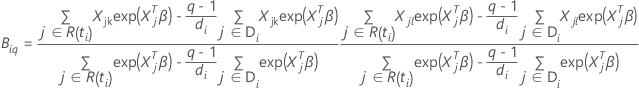
Aproximación de Breslow para datos con empates
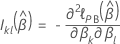
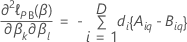
donde
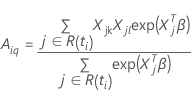
y
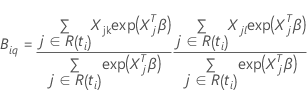
Valor z
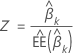
donde  es el error estándar estimado del coeficiente
es el error estándar estimado del coeficiente 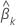 . El valor de
. El valor de  es la raíz cuadrada positiva del késimo elemento diagonal de
es la raíz cuadrada positiva del késimo elemento diagonal de  .
.
CI
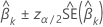
donde 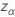 es el punto superior del percentil α de la distribución normal estándar.
es el punto superior del percentil α de la distribución normal estándar.
Valor p

| Término | Description |
|---|---|
 | una variable aleatoria que sigue la distribución normal estándar |
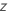 | la estadística de prueba para 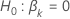 en comparación con la hipótesis alternativa en comparación con la hipótesis alternativa 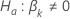 |
Modelos de riesgos proporcionales estratificados
Para un modelo que incluye una variable categórica con niveles s como variable de estratificación, los coeficientes de regresión son constantes en todos los estratos. La estimación de los coeficientes de regresión en el modelo estratificado sigue el mismo proceso que el modelo de riesgos proporcionales sin estratificación. Para el modelo estratificado, la función de verosimilitud logarítmica parcial se expresa de la siguiente forma:

donde 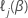 es la verosimilitud logarítmica parcial dentro del estrato j. Sume las derivadas de cada estrato para obtener las ecuaciones de verosimilitud parcial. Las derivadas de cada estrato son las mismas que las derivadas para el modelo de riesgos proporcionales sin estratificación. Los métodos de Breslow y Efron se aplican según corresponda.
es la verosimilitud logarítmica parcial dentro del estrato j. Sume las derivadas de cada estrato para obtener las ecuaciones de verosimilitud parcial. Las derivadas de cada estrato son las mismas que las derivadas para el modelo de riesgos proporcionales sin estratificación. Los métodos de Breslow y Efron se aplican según corresponda.