Ejemplo de Ajuste el Modelo de Cox con Predictores Fijos solamente

Los investigadores médicos quieren determinar si la etapa del cáncer de laringe afecta la probabilidad de muerte. Los investigadores planean ajustar el análisis según la edad del paciente. Los investigadores registran la etapa y la edad de 90 pacientes masculinos con cáncer. Después, los investigadores registran el número de años entre el primer tratamiento y la muerte del paciente o el final del estudio. Finalmente, los investigadores registran si el paciente murió.

Los investigadores médicos realizan la regresión de Cox para evaluar la relación entre la muerte, la edad y la etapa del cáncer. Los investigadores también quieren estimar la probabilidad de supervivencia de un hombre de 60 años para cada etapa.

Nota

Estos datos se adaptaron con base en un conjunto de datos públicos de Kardaun que se encuentran publicados en Klein y Moeschberger (2003)¹. Sin embargo, los resultados de este ejemplo no coinciden con el libro de texto porque el libro de texto utiliza el método Breslow para el manejo de empates y este ejemplo utiliza el método Efron.

Abra los datos de muestra, Cancerdelaringe.MTW.
Elija Estadísticas > Confiabilidad/supervivencia > Regresión de Cox > Modelo de Ajuste de Cox solo con predictores fijos.
En Respuesta, ingrese Tiempo.
En Columna de censura (opcional), ingrese Muerte.
En Predictores continuos, ingrese Edad.
En Predictores categóricos, ingrese Escenario.
Seleccione Gráficas y marque Mostrar gráfica de supervivencia para los valores predictores.
En la lista desplegable, elija Ingresar valores individuales. Ingrese los siguientes valores en la tabla:

Edad Escenario

60 I

60 II

60 III

60 IV
Seleccione Aceptar en cada cuadro de diálogo.

Edad	Escenario
60	I
60	II
60	III
60	IV

Interprete los resultados

Primero, los investigadores utilizan las pruebas de bondad de ajuste para evaluar el ajuste general del modelo. Los valores p para las 3 pruebas son inferiores a 0.05, por lo que los investigadores concluyen que el modelo se ajusta bien a los datos. Luego, los investigadores utilizan la tabla ANOVA para evaluar el efecto de los términos individuales. El valor p para la etapa es significativo a un nivel α de 0.05. Por lo tanto, los investigadores médicos pueden concluir que la etapa del cáncer tiene un efecto estadísticamente significativo en la supervivencia del paciente. Sin embargo, el valor p para la edad es 0.182, por lo que el efecto de la edad no es significativo a un nivel α de 0.05. Los coeficientes para los predictores definen una ecuación que describe la relación entre la etapa, la edad del paciente y el tiempo de supervivencia.

Los investigadores utilizan la tabla de riesgos relativos para predictores categóricos para evaluar el riesgo entre las diferentes etapas del cáncer. Por ejemplo, el riesgo de muerte entre los pacientes en estadio IV es 5.5 veces mayor que el riesgo para los pacientes en estadio I. Además, el intervalo de confianza muestra que el verdadero riesgo de muerte para los pacientes en el estadio IV podría ser de tan solo 2.4 veces o hasta 12.6 veces más que el riesgo para los pacientes en el estadio I, en el nivel de confianza de 95 por ciento. El intervalo de confianza no contiene 1, por lo que la diferencia entre el riesgo de muerte para el estadio I y el estadio IV es estadísticamente significativa.

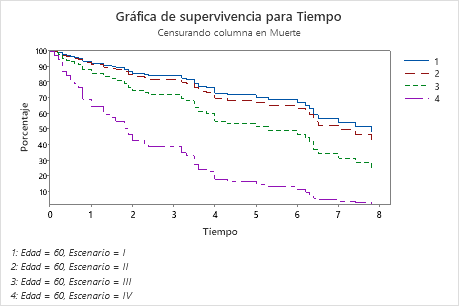
La gráfica de supervivencia muestra la probabilidad de supervivencia de un hombre de 60 años para cada etapa del cáncer durante varios años. Un diagnóstico de cáncer en estadio IV tiene el mayor efecto en la probabilidad de supervivencia. La gráfica muestra que después de 1 año, una edad de 60 años con cáncer en etapa IV tiene solo un 64% de probabilidades de sobrevivir. Las otras tres etapas tienen una probabilidad del 85% o superiores. Después de 2 años, la probabilidad cae a 42% para un paciente con estadio IV, pero se mantiene en 74% o más para las otras tres etapas.

Método

Tipo de modelo de Cox	Solo predictores fijos
Codificación de predictores categóricos	(1, 0)
Ajuste de empate	Efron

Información de censura

Unidades sin censura	Unidades censuradas	Total	Porcentaje censurado
50	40	90	44.44%

Ecuación de regresión

Escenario
I	Puntuación de riesgo	=	0.0 + 0.01903 Edad

II	Puntuación de riesgo	=	0.1400 + 0.01903 Edad

III	Puntuación de riesgo	=	0.6424 + 0.01903 Edad

IV	Puntuación de riesgo	=	1.706 + 0.01903 Edad

Coeficientes

Término	Coef	EE del coef.	Valor Z	Valor p
Edad	0.0190	0.0143	1.33	0.182
Escenario
II	0.140	0.462	0.30	0.762
III	0.642	0.356	1.80	0.071
IV	1.706	0.422	4.04	0.000

Riesgos relativos para predictores continuos

	Unidad de cambio	Riesgo relativo	IC de 95%
Edad	1	1.0192	(0.9911, 1.0481)

Riesgos relativos para predictores categóricos

Nivel A	Nivel B	Riesgo relativo	IC de 95%
Escenario
II	I	1.1503	(0.4647, 2.8477)
III	I	1.9010	(0.9459, 3.8204)
IV	I	5.5068	(2.4086, 12.5901)
III	II	1.6526	(0.6819, 4.0049)
IV	II	4.7872	(1.7825, 12.8566)
IV	III	2.8968	(1.2952, 6.4788)

Resumen del modelo

Modelo	Log-verosimilitud	R-cuadrado	AIC	AICc	BIC
Sin términos	-196.86	—	393.73	393.73	393.73
Con términos	-187.71	18.65%	383.41	384.30	391.06

Pruebas de bondad de ajuste

Prueba	GL	Chi-cuadrada	Valor p
Relación de verosimilitud	4	18.31	0.001
Wald	4	21.15	0.000
Puntuación	4	24.78	0.000

Análisis de Varianza

		Prueba de Wald
Fuente	GL	Chi-cuadrada	Valor p
Edad	1	1.78	0.182
Escenario	3	17.92	0.000

¹ Klein, J.P. & Moeschberger, M.L. (2003). Examples of survival data: Death times of male laryngeal cancer patients. Survival Analysis: Techniques for Censored and Truncated Data (2nd ed., pp. 9-10). Springer.