Para cada sujeto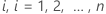 
sea 
la función escalonada que representa el número de eventos que el sujeto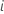 
experimenta hasta el tiempo 
. Entonces: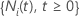
representa un proceso de conteo para el sujeto 
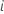. Sea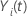 
una variable indicadora que tenga el valor 1 si el sujeto i está en riesgo en el momento t y 0 en caso contrario, que es equivalente a 
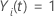si 
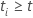y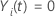 
en caso contrario.
para un individuo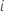 
con un vector de valores predictivos 
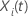, se expresa de la siguiente forma:
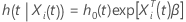
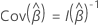
donde 
es la tasa de riesgo inicial que caracteriza la distribución no especificada del tiempo de supervivencia y 
es un vector del componente p de coeficientes de regresión desconocidos.
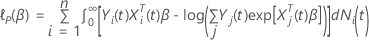
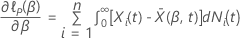
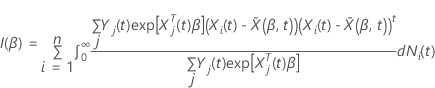
, se expresa de la siguiente forma:
, se expresa de la siguiente forma:
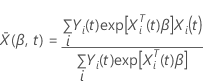
- El sujeto puede experimentar más de un evento de interés.
- El sujeto puede experimentar un evento varias veces. Esta afirmación significa que la variable indicadora que identifica si el sujeto está en riesgo,
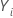, puede cambiar los estados de 1 a 0 y viceversa, varias veces. - El sujeto puede ingresar al estudio después del tiempo 0. Esta afirmación es equivalente a la idea de que un sujeto puede integrarse al conjunto de riesgo después del tiempo 0. Un tiempo se trunca a la izquierda cuando el sujeto ingresa después del tiempo 0.
El formato para ingreso de datos del proceso de conteo
En el formato para ingreso de datos del proceso de conteo, el sujeto está representado en múltiples filas. Cada fila describe un intervalo de tiempo donde los valores de todas las variables son constantes. Los predictores dependientes del tiempo cambian entre filas. Los intervalos comienzan justo después del tiempo de inicio e incluyen el tiempo final. El tiempo de inicio para el intervalo es el tiempo de entrada del sujeto. El tiempo final es la variable de respuesta del sujeto. La columna de censura indica que cualquiera fila donde el tiempo final no es un tiempo de evento.
Observaciones correlacionadas y estimador robusto de covarianza
Aunque varias filas representan a cada sujeto en el formato para ingreso de datos del proceso de conteo, solo una fila de observaciones por sujeto contribuye a la verosimilitud en cada tiempo, a menos que exista correlación entre las observaciones en un subgrupo que pertenezca a cada sujeto. Por ejemplo, las observaciones del sujeto se correlacionan en modelos que incluyen eventos repetidos o recurrentes. Lin and Wei (1989)4 proponen un ajuste de la matriz de covarianza para tomar en cuenta la correlación entre las observaciones interiores del sujeto. Sea 
la matriz de residuos de puntuación. Entonces, la matriz robusta de varianza y covarianza se expresa de la siguiente forma:
donde 
y 
es la matriz de residuos de puntuación con vista contraída. Para obtener la matriz de residuos de puntuación con vista contraída, sustituya todos los conglomerados de filas de residuos de puntuación con la suma de esas filas de residuos.
- Los cálculos para inferencias utilizan la matriz robusta de varianza y covarianza.
- Las pruebas de Wald y Score de la tabla de bondad de ajuste utilizan la matriz robusta de varianza y covarianza. La prueba de relación de verosimilitud no aparece en la tabla de bondad de ajuste debido a que esta prueba asume que las observaciones al interior de un conglomerado son independientes.
- La tabla ANOVA solo puede utilizar la prueba de Wald.
