Métodos y fórmulas para modelos de pruebas aceleradas de vida útil en Plan de pruebas aceleradas de vida útil

Lineal

Término	Description
Y_p	tiempo de falla o logaritmo de tiempo de falla
β₀	intersección de y (constante)
β₁	coeficiente de regresión
σ	recíproca del parámetro de forma (distribución de Weibull) o del parámetro de escala (otras distribuciones)
Φ^-1(p)	el cuantil p ésimo de la distribución de vida útil estadarizada

donde el valor del numerador (11604.53) es el valor inverso de la constante de Boltzman y el valor en el denominador (273.16) es 0 absoluto.

Término	Description
Y_p	tiempo de falla o logaritmo de tiempo de falla
β₀	intersección de y (constante)
β₁	coeficiente de regresión
σ	recíproca del parámetro de forma (distribución de Weibull) o del parámetro de escala (otras distribuciones)
Φ^-1(p)	el cuantil p ésimo de la distribución de vida útil estadarizada

Término	Description
Y_p	tiempo de falla o logaritmo de tiempo de falla
β₀	intersección de y (constante)
β₁	coeficiente de regresión
σ	recíproca del parámetro de forma (distribución de Weibull) o del parámetro de escala (otras distribuciones)
Φ^-1(p)	el cuantil p ésimo de la distribución de vida útil estadarizada

Término	Description
Y_p	tiempo de falla o logaritmo de tiempo de falla
β₀	intersección de y (constante)
β₁	coeficiente de regresión
σ	recíproca del parámetro de forma (distribución de Weibull) o del parámetro de escala (otras distribuciones)
Φ^-1(p)	el cuantil p ésimo de la distribución de vida útil estadarizada

La aceleración estandarizada se calcula de la siguiente manera:

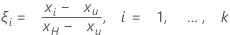
El modelo de pruebas aceleradas de vida útil estandarizado es:

Término	Description
k	número de niveles de la variable de aceleración (sin incluir el nivel de uso normal)
X_i	nivel de la variable de aceleración
X_U	nivel de uso
X_H	nivel más alto de la variable de aceleración