Minitab calcula 3 tipos de residuos.
Residuos regulares
Un residuo es la diferencia entre un valor observado (y) y su valor ajustado correspondiente (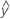
).
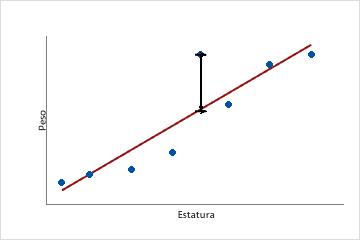
Por ejemplo, esta gráfica de dispersión grafica el peso de las personas en función de su estatura. La línea de regresión ajustada grafica los valores ajustados de peso para cada valor observado de estatura. Supongamos que una persona tiene una estatura de 6 pies y el valor ajustado de su peso es 190 libras. Si su peso real es 200, el residuo es 10.
Grafique los residuos y utilice otros estadísticos de diagnóstico para determinar si el modelo es adecuado y si se cumplen los supuestos de la regresión. Los residuos también pueden identificar qué proporción de la variación en los datos observados es explicada por un modelo.
Residuos estandarizados
El residuo estandarizado es igual al valor de un residuo, ei, dividido entre una estimación de su desviación estándar. Los residuos estandarizados mayores que 2 y menores que -2 suelen considerarse grandes y Minitab identifica estas observaciones con una 'R' en la tabla de observaciones poco comunes y en la tabla de ajustes y residuos. Las observaciones que Minitab etiqueta no siguen adecuadamente la ecuación de regresión propuesta. Sin embargo, se espera que haya algunas observaciones poco comunes. Por ejemplo, con base en los criterios para los residuos estandarizados grandes, se esperaría que aproximadamente el 5% de las observaciones se marque como observaciones que tienen un residuo estandarizado grande.
Utilice el residuo estandarizado como ayuda para detectar valores atípicos. La estandarización de los residuos es útil porque los residuales sin procesar podrían no ser identificadores aceptables de valores atípicos cuando tienen varianza no constante. Si los residuos con los valores de X más distantes de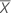 
tienen mayor varianza que los residuos con los valores de X más cercanos a 
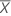, entonces los valores atípicos son más difíciles de detectar. La estandarización controla esta varianza no constante y todos los residuos estandarizados tienen la misma desviación estándar.
Los residuos estandarizados también se denominan residuos studentizados internamente.
Residuos eliminados studentizados
Los residuos eliminados studentizados de una observación se calculan dividiendo el residuo eliminado de una observación entre una estimación de su desviación estándar. Un residuo eliminado di es la diferencia entre yi y su valor ajustado en un modelo que omite la observación iésima de sus cálculos. La observación se omite para determinar cómo se comporta el modelo sin este posible valor atípico. Si una observación tiene un residuo eliminado studentizado grande (si su valor absoluto es mayor que 2), podría tratarse de un valor atípico en los datos.
Utilice el residuo eliminado como ayuda para detectar valores atípicos. Los residuos eliminados son útiles porque los residuos sin procesar podrían no ser identificadores aceptables de valores atípicos cuando tienen varianza no constante. Si los residuos con los valores de X más distantes de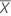 
tienen mayor varianza que los residuos con los valores de X más cercanos a 
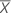, entonces los valores atípicos son más difíciles de detectar. Todos los residuos eliminados tienen la misma desviación estándar.
Cada residuo eliminado studentizado sigue la distribución t con (n – 1 – p) grados de libertad, donde p es igual al número de términos en el modelo de regresión.
Los residuos eliminados studentizados también se denominan residuos studentizados externamente o residuos t eliminados.
