Existen dos condiciones que impiden la convergencia de las estimaciones de máxima verosimilitud para los coeficientes: separación completa y separación casi completa.
Separación completa
La separación completa ocurre cuando una combinación lineal de los predictores produce una predicción perfecta de la variable de respuesta. Por ejemplo, en el siguiente conjunto de datos, si X ≤ 4, entonces Y = 0. Si X > 4, entonces Y = 1.
| Y | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
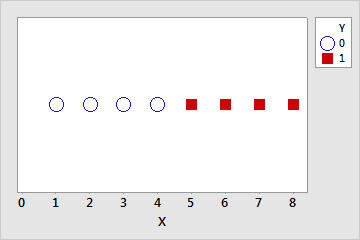
Separación casi completa
La separación casi completa es similar a la separación completa. Los predictores producen una predicción perfecta de la variable de respuesta para la mayoría de los valores de los predictores, pero no todos. Por ejemplo, en el conjunto de datos anterior, para uno de los valores donde X = 4, sea Y = 1 en lugar de 0. Ahora, si X < 4, entonces Y = 0, si X > 4, entonces Y = 1, pero si X = 4, entonces Y podría ser 0 o 1. Esta superposición en el rango medio de los datos hace que la separación sea casi completa.
| Y | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |

Causas y solución
Con frecuencia, la separación se produce cuando el conjunto de datos es demasiado pequeño para observar eventos con bajas probabilidades. Mientras más predictores haya en el modelo, más probable será que ocurra la separación, porque los grupos individuales de los datos tienen tamaños de muestra más pequeños.
Aunque Minitab genera una advertencia cuando detecta separación, mientras más predictores haya en el modelo, más difícil será identificar la causa de la separación. La inclusión de términos de interacción en el modelo hace que la dificultad sea aún mayor.
- Aumente la cantidad de datos. La separación suele producirse cuando hay una categoría o rango de un predictor que solo tiene un valor de la respuesta. Un tamaño de muestra mayor aumenta la probabilidad de diferentes valores para la respuesta.
- Considere lo que significa la separación. Aunque la separación completa y separación casi completa pueden indicar que el tamaño de la muestra es demasiado pequeño, también pueden indicar relaciones importantes. Si la probabilidad real de un evento en un nivel o combinación de niveles específicos está cerca de 0 o 1, esta información es importante.
- Considere un modelo alternativo. Mientras más términos haya en el modelo, más probable será que se produzca separación para al menos una variable. Al seleccionar los términos para el modelo, puede comprobar si la exclusión de un término permite que las estimaciones de máxima verosimilitud converjan. Si existe un modelo útil que no utilice el término, puede continuar el análisis con el nuevo modelo.
- Verifique si puede combinar categorías en las variables problemáticas. Si hay categorías que sea razonable combinar, la separación puede desaparecer del conjunto de datos. Por ejemplo, supongamos que “Frutas” es una variable incluida en el modelo. “Toronja” no tiene ningún evento debido al reducido número de ensayos. Combinar “Toronja” y “Naranjas” en la categoría “Cítricos” elimina la separación.
Table 1. Datos con separación completa Frutas Eventos Ensayos Toronja 0 10 Naranjas 5 100 Manzanas 25 100 Bananas 40 100 Table 2. Datos con superposición Frutas Eventos Ensayos Cítricos 5 110 Manzanas 25 100 Bananas 40 100 - Verifique si una variable categórica problemática es una variable agregada. Si la relación de la variable no agregada con la respuesta no muestra separación completa, la sustitución de los datos numéricos puede eliminar la separación. Por ejemplo, supongamos que “Duración del empleo” es una variable agregada en el modelo. Cuando los datos están en incrementos de 30 días, el nivel más bajo tiene todos los eventos y el nivel más alto no tiene ningún evento, lo que crea separación completa. La sustitución del número de días en el modelo elimina la separación.
Table 3. Datos con separación completa Categorías de duración Eventos Ensayos 1–90 2 2 91–180 1 2 181–270 1 2 271–360 0 2 Duración exacta Eventos Ensayos 45 1 1 60 1 1 95 1 1 176 0 1 185 0 1 241 1 1 280 0 1 299 0 1
Lectura recomendada
Para obtener más información acerca de la separación, por favor, consulte Albert y J. A. Anderson (1984) "On the existence of maximum likelihood estimates in logistic regression models" Biometrika 71, 1, 1–10.
